题目内容
已知△ABC中内角A，B，C的对边分别为a，b，c，向量| m |
| 3 |
| n |
| B |
| 2 |
| m |
| n |
（1）求锐角B的大小；
（2）如果b=2，求△ABC的面积S△ABC的最大值．
分析：（1）根据
⊥
，
=(2sinB，
)，
=(2cos2
-1，cos2B)
•
=0可得，2sin(2B+
)=0，又因为0＜B＜
，得到答案B=
．
（2）根据余弦定理可得b2=a2+c2-2accosB，有根据基本不等式可知22=a2+c2-ac≥2ac-ac=ac∴ac≤4（当且仅当a=c时取到等号）
代入s△ABC=
acsinB=
ac≤
，得到答案．
| m |
| n |
| m |
| 3 |
| n |
| B |
| 2 |
| m |
| n |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
（2）根据余弦定理可得b2=a2+c2-2accosB，有根据基本不等式可知22=a2+c2-ac≥2ac-ac=ac∴ac≤4（当且仅当a=c时取到等号）
代入s△ABC=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
解答：解：（1）∵
⊥
，
=(2sinB，
)，
=(2cos2
-1，cos2B)
•
=0
•
=(2sinB，
)•(2cos2
-1，cos2B)
=2sinB(2cos2
-1)+
cos2B_ =sin2B+
cos2B
=2sin(2B+
)=0
又∵0＜B＜
，∴2B+
=π，∴B=
（2）由余弦定理得b2=a2+c2-2accosB
∴22=a2+c2-ac≥2ac-ac=ac∴ac≤4（当且仅当a=c时取到等号）
∴s△ABC=
acsinB=
ac≤
∴△ABC的面积S△ABC的最大值为
| m |
| n |
| m |
| 3 |
| n |
| B |
| 2 |
| m |
| n |
| m |
| n |
| 3 |
| B |
| 2 |
=2sinB(2cos2
| B |
| 2 |
| 3 |
| 3 |
=2sin(2B+
| π |
| 3 |
又∵0＜B＜
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
（2）由余弦定理得b2=a2+c2-2accosB
∴22=a2+c2-ac≥2ac-ac=ac∴ac≤4（当且仅当a=c时取到等号）
∴s△ABC=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
| 3 |
点评：本题主要考查向量数量积和向量垂直之间的关系．即两向量互相垂直时二者的数量积等于0．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
，
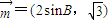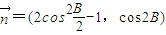，且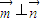
．