题目内容
 如图,△ABC的外接圆⊙O的半径为
如图,△ABC的外接圆⊙O的半径为| 5 |
| ||
| 21 |
(1)求证:平面ADC⊥平面BCDE;
(2)求几何体ABCDE的体积;
(3)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为
| 2 |
| 7 |
分析:(1)由已知中CD⊥⊙O所在的平面,BE∥CD,易得BE⊥平面ABC,则BE⊥AB,由BE=1,cos∠AEB=
,易得AB是⊙O的直径,则AC⊥BC由线面垂直的判定定理可得CD⊥平面ABC,再由面面垂直的判定定理可得平面ADC⊥平面BCDE;
(2)由(1)中结论,可得AC⊥平面BCDE,求出平面BCDE的面积和AC的长,代入棱锥体积公式,即可求出几何体ABCDE的体积;
(3)方法一:过点M作MN⊥CD于N,连接AN,作MF⊥CB于F,连接AF,可得∠MAN为MA与平面ACD所成的角,设MN=x,则由直线AM与平面ACD所成角的正弦值为
,我们可以构造关于x的方程,解方程即可求出x值,进而得到点M的位置.
方法二:建立如图所示空间直角坐标系C-xyz,求出平面ABC的法向量和直线AM的方向向量(含参数λ),由直线AM与平面ACD所成角的正弦值为
,根据向量夹角公式,我们可以构造关于λ的方程,解方程即可得到λ值,进而得到点M的位置.
| ||
| 21 |
(2)由(1)中结论,可得AC⊥平面BCDE,求出平面BCDE的面积和AC的长,代入棱锥体积公式,即可求出几何体ABCDE的体积;
(3)方法一:过点M作MN⊥CD于N,连接AN,作MF⊥CB于F,连接AF,可得∠MAN为MA与平面ACD所成的角,设MN=x,则由直线AM与平面ACD所成角的正弦值为
| 2 |
| 7 |
方法二:建立如图所示空间直角坐标系C-xyz,求出平面ABC的法向量和直线AM的方向向量(含参数λ),由直线AM与平面ACD所成角的正弦值为
| 2 |
| 7 |
解答: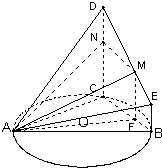 解:(1)∵CD⊥平面ABC,BE∥CD
解:(1)∵CD⊥平面ABC,BE∥CD
∴BE⊥平面ABC,∴BE⊥AB …(1分)
∴cos∠AEB=
=
∵BE=1∴AE=
,
从而AB=
=2
…(2分)
∵⊙O的半径为
,
∴AB是直径,∴AC⊥BC…(3分)
又∵CD⊥平面ABC,
∴CD⊥BC,故BC⊥平面ACD
∵BC?平面BCDE,
∴平面ADC⊥平面BCDE …(5分)
(2)由(1)知:AC=
=4,…(6分)
VABCDE=
SBCDE•AC=
×
(BE+CD)•BC•AC=
(1+4)•2•4=
…(9分)
(3)方法一:
假设点M存在,过点M作MN⊥CD于N,连接AN,作MF⊥CB于F,连接AF
∵平面ADC⊥平面BCDE,∴MN⊥平面ACD,
∴∠MAN为MA与平面ACD所成的角 …(10分)
设MN=x,计算易得,DN=
x,MF=4-
x…(11分)
故AM=
=
=
sin∠MAN=
=
=
…(12分)
解得:x=-
(舍去) x=
,…(13分)
故MN=
CB,从而满足条件的点M存在,且DM=
DE…(14分)
方法二:建立如图所示空间直角坐标系C-xyz,则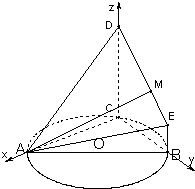 :
:
A(4,0,0),B(0,2,0),D(0,0,4),E(0,2,1),O(0,0,0)
则
=(0,2,-3)…(10分)
易知平面ACD的法向量为
=(0,2,0),
假设M点存在,设M(a,b,c),则
=(a,b,c-4),
再设
=λ
,λ∈(0,1]∴
⇒
,
即M(0,2λ,4-3λ),从而
=(-4,2λ,4-3λ)
…(11分)
设直线AM与平面ABD所成的角为θ,
则:sinθ=|cos?
,
>|=
=
…(12分)
解得λ=-
或λ=
,…(13分)
其中λ=-
∉(0,1]应舍去,而λ=
∈(0,1]
故满足条件的点M存在,且点M的坐标为(0,
,2)…(14分)
 解:(1)∵CD⊥平面ABC,BE∥CD
解:(1)∵CD⊥平面ABC,BE∥CD∴BE⊥平面ABC,∴BE⊥AB …(1分)
∴cos∠AEB=
| BE |
| AE |
| ||
| 21 |
∵BE=1∴AE=
| 21 |
从而AB=
| AE2-BE2 |
| 5 |
∵⊙O的半径为
| 5 |
∴AB是直径,∴AC⊥BC…(3分)
又∵CD⊥平面ABC,
∴CD⊥BC,故BC⊥平面ACD
∵BC?平面BCDE,
∴平面ADC⊥平面BCDE …(5分)
(2)由(1)知:AC=
| AB2-BC2 |
VABCDE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 20 |
| 3 |
(3)方法一:
假设点M存在,过点M作MN⊥CD于N,连接AN,作MF⊥CB于F,连接AF
∵平面ADC⊥平面BCDE,∴MN⊥平面ACD,
∴∠MAN为MA与平面ACD所成的角 …(10分)
设MN=x,计算易得,DN=
| 3 |
| 2 |
| 3 |
| 2 |
故AM=
| AF2+MF2 |
| AC2+CF2+MF2 |
16+x2+(4-
|
| MN |
| AM |
| x | ||||
|
| 2 |
| 7 |
解得:x=-
| 8 |
| 3 |
| 4 |
| 3 |
故MN=
| 2 |
| 3 |
| 2 |
| 3 |
方法二:建立如图所示空间直角坐标系C-xyz,则
 :
:A(4,0,0),B(0,2,0),D(0,0,4),E(0,2,1),O(0,0,0)
则
| DE |
易知平面ACD的法向量为
| OB |
假设M点存在,设M(a,b,c),则
| DM |
再设
| DM |
| DE |
|
|
即M(0,2λ,4-3λ),从而
| AM |
…(11分)
设直线AM与平面ABD所成的角为θ,
则:sinθ=|cos?
| AM |
| OB |
| |2λ×2| | ||
2•
|
| 2 |
| 7 |
解得λ=-
| 4 |
| 3 |
| 2 |
| 3 |
其中λ=-
| 4 |
| 3 |
| 2 |
| 3 |
故满足条件的点M存在,且点M的坐标为(0,
| 4 |
| 3 |
点评:本题考查的知识点是直线与平面所成的角,棱锥的体积,平面与平面垂直的判定,其中(1)的关键是证得CD⊥平面ABC,(2)的关键是得到几何体是一个以AC为高,以BCDE为底面的四棱锥,(3)的关键是直线AM与平面ACD所成角的正弦值为
,构造满足条件的方程.
| 2 |
| 7 |

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
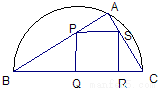
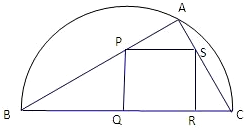 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=20米,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=20米,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值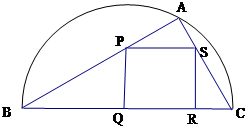 如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC的内接正方形PQRS为一水池,△ABC外的地方种草,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值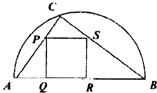 如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值
如图,某小区准备绿化一块直径为AB的半圆形空地,点C在半圆弧上,半圆内△ABC外的地方种草,△ABC的内接正方形PQRS内部为一水池,其余地方种花,若AB=2a,∠CAB=θ,设△ABC的面积为S1,正方形PQRS的边长为x,面积为S2,将比值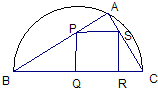 (2007•杨浦区二模)如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值
(2007•杨浦区二模)如图,某小区准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余地方种花.若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形PQRS的面积为S2,将比值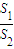 称为“规划合理度”.
称为“规划合理度”.