题目内容
当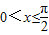 时,关于x的方程cos2x-sinx+a=0时有解,则a的取值范围是 .
时,关于x的方程cos2x-sinx+a=0时有解,则a的取值范围是 .
【答案】分析:先利用同角三角函数关系式把所给方程中的三角函数名统一,方程可化为关于sinx的一元二次方程,把a用含sinx的式子表示,根据正弦函数的有界性,求出这个含sinx的式子的范围,即可得到a的范围.
解答:解:cos2x-sinx+a=0可化简为sin2x+sinx-a-1=0
即(sinx+ )2-a-
)2-a- =0在
=0在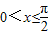 时有解
时有解
当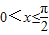 时,0<sinx≤1,∴
时,0<sinx≤1,∴ <(sinx+
<(sinx+ )2≤
)2≤
∴ <a+
<a+ ≤
≤ ,-1<a≤1
,-1<a≤1
∴a的取值范围是(-1,1]
故答案为(-1,1]
点评:本题主要考查了含有正弦的函数值域的求法,用到了正弦函数的有界性,属于三角函数的常规题.
解答:解:cos2x-sinx+a=0可化简为sin2x+sinx-a-1=0
即(sinx+
 )2-a-
)2-a- =0在
=0在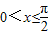 时有解
时有解当
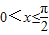 时,0<sinx≤1,∴
时,0<sinx≤1,∴ <(sinx+
<(sinx+ )2≤
)2≤
∴
 <a+
<a+ ≤
≤ ,-1<a≤1
,-1<a≤1∴a的取值范围是(-1,1]
故答案为(-1,1]
点评:本题主要考查了含有正弦的函数值域的求法,用到了正弦函数的有界性,属于三角函数的常规题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上的函数
上的函数 则
则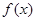 的值域为
的值域为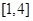
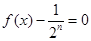 (
(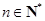 )有4个不相等的实数根
)有4个不相等的实数根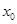 ,使得不等式
,使得不等式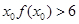 成立
成立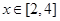 时,函数
时,函数 是定义在R上的周期函数,周期为
是定义在R上的周期函数,周期为 ,对
,对 都有
都有 ,且当
,且当 时,
时, ,若在区间
,若在区间 内关于x的方程
内关于x的方程 =0
=0 恰有3个不同的实根,则a的取值范围是( )
恰有3个不同的实根,则a的取值范围是( ) C.
C. D.
D.
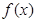 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意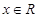 ,都有
,都有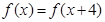 ,且当
,且当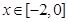 时,
时,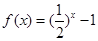 ,若在区间
,若在区间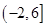 内关于x的方程
内关于x的方程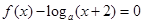
 恰有3个不同的实数根,则a的取值范围是( )
恰有3个不同的实数根,则a的取值范围是( )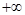 ) C.
) C.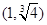 D.
D.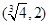
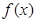 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意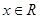 ,都有
,都有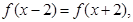 且
且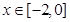 时,
时,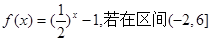 内关于x的方程
内关于x的方程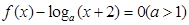 恰有3个不同的实数根,则a的取值范围是 ( )
恰有3个不同的实数根,则a的取值范围是 ( )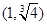 B.
B.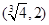 C.(1,2) D.
C.(1,2) D.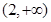
 是R上的偶函数,对任意
是R上的偶函数,对任意 ,都有
,都有 且当
且当 时,
时, 内关于x的方程
内关于x的方程 恰有3个不同的实数根,则a的取值范围是( )
恰有3个不同的实数根,则a的取值范围是( ) C.
C. D.
D.