题目内容
(本题满分8分)求过点A(2,-1),且和直线x-y=1相切,圆心在直线y=-2x上的圆的方程.
【答案】
(x-1)2+(y+2)2=2或(x-9)2+(y+18)2=338.
【解析】
试题分析:因为圆心C在直线y=-2x上,可设圆心为C(a,-2a).
则点C到直线x-y=1的距离d=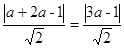
根据题意,d=|AC|,则 =(a-2)2+(-2a+1)2,所以a2-2a+1=0,所以a=1或a=9.
=(a-2)2+(-2a+1)2,所以a2-2a+1=0,所以a=1或a=9.
当a=1时,所以圆心为C(1,-2),半径r=d= ,所以所求圆的方程是(x-1)2+( y+2)2=2 ;
,所以所求圆的方程是(x-1)2+( y+2)2=2 ;
当a=9时,圆心为C(9,-18),半径r=d=13 ,所以所求圆的方程是 (x-9)2+(y+18)2=338.
,所以所求圆的方程是 (x-9)2+(y+18)2=338.
考点:圆的方程的求法;直线与圆的位置关系;点到直线的距离公式;两点间的距离公式。
点评:要求圆的标准方程,只需要确定两个量:圆心和半径。此题灵活应用圆的性质确定圆心和半径是解题的关键。

练习册系列答案
相关题目
 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度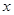 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 千米/小时;当车流密度不超过
千米/小时;当车流密度不超过 辆/千米时,车流速度为
辆/千米时,车流速度为 千米/小时,研究表明;当
千米/小时,研究表明;当 时,车流速度
时,车流速度 的表达式;
的表达式; 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).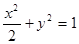 ,直线
,直线 过右焦点
过右焦点 ,与椭圆交于
,与椭圆交于 两点.
两点. 时,求线段
时,求线段 的长度;
的长度; 时,求直线
时,求直线