题目内容
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2个小题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系 中,把矩阵
中,把矩阵 确定的压缩变换
确定的压缩变换 与矩阵
与矩阵 确定的旋转变换
确定的旋转变换 进行复合,得到复合变换
进行复合,得到复合变换 .
.
(Ⅰ)求复合变换 的坐标变换公式;
的坐标变换公式;
(Ⅱ)求圆
 在复合变换
在复合变换 的作用下所得曲线
的作用下所得曲线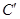 的方程.
的方程.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),
为参数), 、
、 分别为直线
分别为直线 与
与 轴、
轴、 轴的交点,线段
轴的交点,线段 的中点为
的中点为 .
.
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,求点
轴的正半轴为极轴建立极坐标系,求点 的极坐标和直线
的极坐标和直线 的极坐标方程.
的极坐标方程.
(3)(本小题满分7分)选修4—5:不等式选讲
已知不等式 的解集与关于
的解集与关于 的不等式
的不等式 的解集相等.
的解集相等.
(Ⅰ)求实数 ,
, 的值;
的值;
(Ⅱ)求函数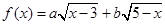 的最大值,以及取得最大值时
的最大值,以及取得最大值时 的值.
的值.
(1)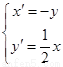 ,
,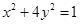 (2)
(2) 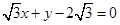 ,
,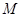 的极坐标为
的极坐标为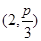 ,
, 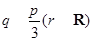
(3)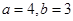 ,
, 时,函数取得最大值
时,函数取得最大值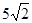
【解析】
试题分析:本小题主要考查矩阵与变换等基础知识,考查运算求解能力及函数与方程思想.满分7分.
解:(Ⅰ)复合变换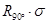 对应的矩阵为
对应的矩阵为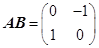
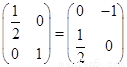 ,……2分
,……2分
所以,复合变换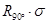 的坐标变换公式为
的坐标变换公式为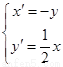 . ……………3分
. ……………3分
(Ⅱ)设圆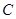 上任意一点
上任意一点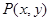 在变换
在变换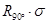 的作用下所得的点为
的作用下所得的点为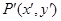 ,
,
由(Ⅰ)得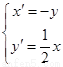 ,即
,即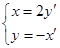 ,………………5分
,………………5分
代入圆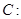
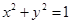 ,得
,得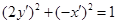 ,
,
所以,曲线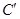 的方程是
的方程是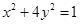 .…………………7分
.…………………7分
(2)(本小题满分7分)选修4—4:坐标系与参数方程
本小题主要考查参数方程、极坐标方程等基础知识,考查运算求解能力以及化归与转化思想.满分7分.
(3)(本小题满分7分)选修4—5:不等式选讲
本小题主要考查绝对值的含义、柯西不等式等基础知识,考查运算求解能力以及推理论证能力,考查函数与方程思想.满分7分.
(Ⅰ)∵不等式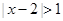 的解集为
的解集为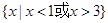 ,……………………1分
,……………………1分
∴不等式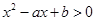 的解集为
的解集为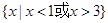 .
.
从而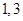 为方程
为方程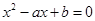 的两根,………………2分
的两根,………………2分
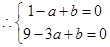 ,
,
解得: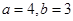 .……………………3分
.……………………3分
(Ⅱ)函数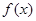 的定义域为
的定义域为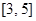 ,且显然有
,且显然有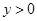 ,
,
由柯西不等式可得: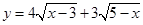
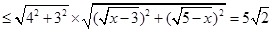 ,……………5分
,……………5分
当且仅当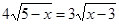 时等号成立, ……………6分
时等号成立, ……………6分
即 时,函数取得最大值
时,函数取得最大值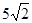 .………………7分
.………………7分
考点:矩阵与变换,绝对值的含义、柯西不等式等基础知识,参数方程、极坐标方程等基础知识。
点评:主要是考查了考查三选一中矩阵与变换、绝对值、柯西不等式知识点的运算求解能力及函数与方程思想,以及化归与转化思想.
