题目内容
 如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是
如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是①③
①③
.①动点A′在平面ABC上的射影在线段AF上;
②BC∥平面A′DE;
③三棱锥A′-FED的体积有最大值.
分析:根据已知结合等腰三角形三线合一,线面垂直及面面垂直的判定定理,可证得平面ABC⊥平面A′GF,进而根据面面垂直的性质可判断①;由A′与A,F两点重合时,BC?平面A′DE可判断②;当平面ABC⊥平面A′DE时,三棱锥A′-FED的高取最大值,三棱锥A′-FED的体积取最大值,可判断③.
解答:解:∵等边三角形ABC的中线AF与中位线DE交于点G,
∴G为AF和DE的中点,且AF⊥DE于G点
则△A′DE与△FDE均为等边三角形,
∴A′G⊥DE且FG⊥DE
又∵A′G∩FG=G,A′G,FG?平面A′GF
∴DE⊥平面A′GF
又由DE?平面ABC
∴平面ABC⊥平面A′GF
故动点A′在平面ABC上的射影在两个平面的交线线段AF上;故①正确
由BC∥DE,当BC?平面A′DE,即A′与A,F两点不重合时,BC∥平面A′DE;
但A′与A,F两点重合时,BC?平面A′DE;故②错误
当平面ABC⊥平面A′DE时,三棱锥A′-FED的高取最大值,三棱锥A′-FED的体积取最大值.故③正确
故正确的命题有①③
故答案为:①③
∴G为AF和DE的中点,且AF⊥DE于G点
则△A′DE与△FDE均为等边三角形,
∴A′G⊥DE且FG⊥DE
又∵A′G∩FG=G,A′G,FG?平面A′GF
∴DE⊥平面A′GF
又由DE?平面ABC
∴平面ABC⊥平面A′GF
故动点A′在平面ABC上的射影在两个平面的交线线段AF上;故①正确
由BC∥DE,当BC?平面A′DE,即A′与A,F两点不重合时,BC∥平面A′DE;
但A′与A,F两点重合时,BC?平面A′DE;故②错误
当平面ABC⊥平面A′DE时,三棱锥A′-FED的高取最大值,三棱锥A′-FED的体积取最大值.故③正确
故正确的命题有①③
故答案为:①③
点评:本题以命题的真假判断为载体,考查了直线与平面平行的判定,线面垂直,面面垂直的判定与性质,棱锥的体积,难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 8、如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )
8、如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )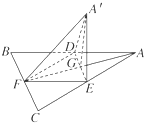

 如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )
如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )