题目内容
设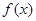 、
、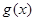 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当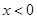 时,
时,
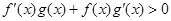 .且
.且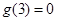 .则不等式
.则不等式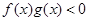 的解集是 ( )
的解集是 ( )
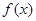 、
、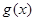 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当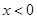 时,
时, 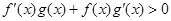 .且
.且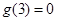 .则不等式
.则不等式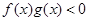 的解集是 ( )
的解集是 ( )| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0, 3) |
| C.(-∞ ,- 3)∪(3,+∞) | D.(-∞,- 3)∪(0, 3) |
D
本题考查函数奇偶性,单调性,导数运算,能利用函数单调性解不等式.
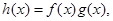 则
则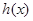 是R上的奇函数;因为当
是R上的奇函数;因为当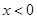 时
时
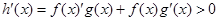 ,所以函数
,所以函数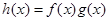 在
在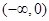 上是增函数;所以
上是增函数;所以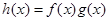 在
在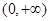 上是增函数;
上是增函数;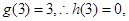 则
则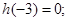 不等式
不等式
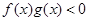 即为
即为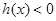 可化为
可化为 ,解得
,解得
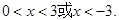 故选D
故选D
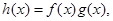 则
则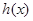 是R上的奇函数;因为当
是R上的奇函数;因为当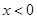 时
时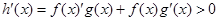 ,所以函数
,所以函数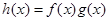 在
在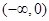 上是增函数;所以
上是增函数;所以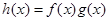 在
在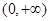 上是增函数;
上是增函数;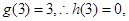 则
则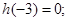 不等式
不等式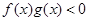 即为
即为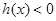 可化为
可化为 ,解得
,解得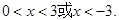 故选D
故选D
练习册系列答案
相关题目
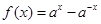
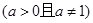 在
在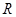 上是增函数,那么
上是增函数,那么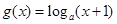 的大致图象是( )
的大致图象是( )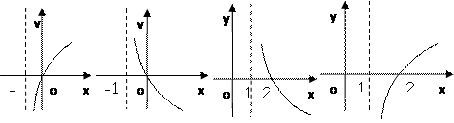
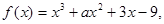 已知
已知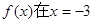 时取得极值,则
时取得极值,则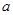 = ( )
= ( )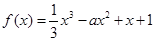 在
在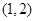 上单调递减,则
上单调递减,则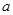 的取值范围是( )
的取值范围是( )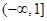
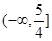
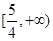
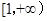
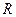 上偶函数
上偶函数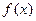 ,且
,且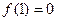 ,当
,当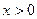 时有
时有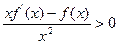 ,则不等式
,则不等式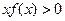 解集为_______
解集为_______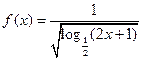 的定义域为 ▲
的定义域为 ▲ 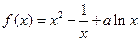 在
在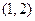 上存在单调递增区间的充要条件是
上存在单调递增区间的充要条件是 ):
):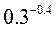
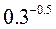 ;
;