题目内容
圆x2+y2=r2在点(x0,y0)处的切线方程为x0x+y0y=r2,类似的,可以求得椭圆
+
=1在(2,1)处的切线方程为______.
| x2 |
| 8 |
| y2 |
| 2 |
圆x2+y2=r2的方程,可写成x•x+y•y=r2,在点(x0,y0)处的切线方程为x0x+y0y=r2,
类似地,椭圆
+
=1,可写成
+
=1,在点(x0,y0)处的切线方程为
+
=1
∴椭圆
+
=1在(2,1)处的切线方程为
+
=1
即
+
=1
故答案为:
+
=1
类似地,椭圆
| x2 |
| 8 |
| y2 |
| 2 |
| x•x |
| 8 |
| y•y |
| 2 |
| x0•x |
| 8 |
| y0•y |
| 2 |
∴椭圆
| x2 |
| 8 |
| y2 |
| 2 |
| 2x |
| 8 |
| y |
| 2 |
即
| x |
| 4 |
| y |
| 2 |
故答案为:
| x |
| 4 |
| y |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
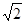 B .0<r<
B .0<r< B、0<r<
B、0<r<