题目内容
（2013•广州一模）如图，一条河的两岸平行，河的宽度d=600m，一艘客船从码头A出发匀速驶往河对岸的码头B．已知|AB|=1km，水流速度为2km/h，若客船行驶完航程所用最短时间为6分钟，则客船在静水中的速度大小为（ ）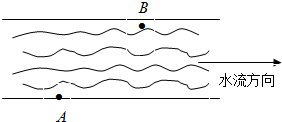
分析：设客船在静水中的速度大小为
km/h，水流速度为
，则|
|=2km/h，则船实际航行的速度
=
+
，t=
=0.1h．把船在静水中的速度正交分解为
=
+
．利用
客船行驶完航程所用最短时间为6分钟，即可分别得出
及
．再利用向量的运算法则和向量模的计算公式、即可得出．
| v静 |
| v水 |
| v水 |
| v |
| v静 |
| v水 |
| 6 |
| 60 |
| v静 |
| vx |
| vy |
客船行驶完航程所用最短时间为6分钟，即可分别得出
| vy |
| vx |
解答：解：设客船在静水中的速度大小为
km/h，水流速度为
，则|
|=2km/h，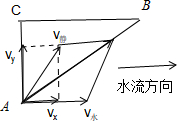
则船实际航行的速度
=
+
，t=
=0.1h．
由题意得|
|≤
=10．
把船在静水中的速度正交分解为
=
+
．
∴
|=
=6，
在Rt△ABC中，BC=
=0.8．
∵|
+
|=|
|+|
=
=8，
∴|
|=8-2=6
∴|
=
=6
．∴
=6
km/h．
设＜
，
＞=θ，则tanθ=
=1，∴cosθ=
．
此时|
|=|
+
|=
=
=
=10≤10，满足条件．
故选B．
| v静 |
| v水 |
| v水 |
则船实际航行的速度
| v |
| v静 |
| v水 |
| 6 |
| 60 |
由题意得|
| v |
|
| ||
| 0.1 |
把船在静水中的速度正交分解为
| v静 |
| vx |
| vy |
∴
| |vy |
| 0.6 |
| 0.1 |
在Rt△ABC中，BC=
| 12-0．62 |
∵|
| vx |
| v水 |
| vx |
| v水| |
| BC |
| 0.1 |
∴|
| vx |
∴|
| v静| |
|
|
| 2 |
| v静 |
| 2 |
设＜
| v静 |
| v水 |
|
| ||
|
|
| ||
| 2 |
此时|
| v |
| v静 |
| v水 |
|
|
(6
|
72+24
|
故选B．
点评：熟练掌握向量的运算法则、向量的正交分解和向量模的计算公式是解题的关键．
练习册系列答案
灵星计算小达人系列答案
相关题目
（2013•广州一模）如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠BCD=60°，AB=2AD，PD⊥平面ABCD，点M为PC的中点．