题目内容
7.设数列{an}满足3a1+32a2+…+3nan=$\frac{{n}^{2}+pn}{2}$(n∈N*,p∈R)(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn,若对于任意的n∈N*,都有Sn<$\frac{5}{4}$成立,求证实数p的取值范围.
分析 (Ⅰ)在原数列递推式中取n=n+1,作差后即可求得数列的通项公式;
(Ⅱ)利用错误相减法求得数列{an}的前n项和Sn,放大后求解不等式$\frac{27-22p}{8}≤\frac{5}{4}$得正实数p的取值范围.
解答 解:(Ⅰ)由3a1+32a2+…+3nan=$\frac{{n}^{2}+pn}{2}$,得$3{a}_{1}=\frac{p+1}{2}$,${a}_{1}=\frac{p+1}{6}$.
再由3a1+32a2+…+3nan=$\frac{{n}^{2}+pn}{2}$,得3a1+32a2+…+3n+1an+1=$\frac{(n+1)^{2}+p(n+1)}{2}$.
两式作差得:${3}^{n+1}{a}_{n+1}=\frac{2n+p+1}{2}$,∴${a}_{n+1}=\frac{2n+p+1}{2}•\frac{1}{{3}^{n+1}}$.
则${a}_{n}=\frac{2n+p-1}{2}•\frac{1}{{3}^{n}}$;
(Ⅱ)${S}_{n}=\frac{2•1+p-1}{2}•\frac{1}{3}+\frac{2•2+p-1}{2}•\frac{1}{{3}^{2}}$$+…+\frac{2n+p-1}{2}•\frac{1}{{3}^{n}}$.
$\frac{1}{3}{S}_{n}=\frac{2•1+p-1}{2}•\frac{1}{{3}^{2}}+\frac{2•2+p-1}{2}•\frac{1}{{3}^{3}}$$+…+\frac{2•(n-1)+p-1}{2}•\frac{1}{{3}^{n}}+\frac{2n+p-1}{2}•\frac{1}{{3}^{n+1}}$.
两式作差得:$\frac{2}{3}{S}_{n}=\frac{p+1}{6}+\frac{1}{2}(\frac{1}{{3}^{2}}+\frac{1}{{3}^{3}}+…+\frac{1}{{3}^{n}})-\frac{2n+p-1}{2}•\frac{1}{{3}^{n+1}}$=$\frac{p+1}{6}+\frac{1}{2}•\frac{\frac{1}{9}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}-\frac{2n+p-1}{2}•\frac{1}{{3}^{n+1}}$.
∴${S}_{n}=\frac{27-22p}{8}-\frac{1}{8}•\frac{1}{{3}^{n-1}}-6n<\frac{27-22p}{8}$.
要使对于任意的n∈N*,都有Sn<$\frac{5}{4}$成立,则
$\frac{27-22p}{8}≤\frac{5}{4}$,解得:$p≥\frac{17}{22}$.
∴正实数p的取值范围是[$\frac{17}{22},+∞$).
点评 本题考查了裂项相消法求数列的通项公式,考查了错位相减法求数列的前n项和,考查了数学转化思想方法,是中高档题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案| A. | $\left\{{\begin{array}{l}{a=-3}\\{b=3}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{a=4}\\{b=-11}\end{array}}\right.$ | ||
| C. | $\left\{{\begin{array}{l}{a=-3}\\{b=3}\end{array}}\right.$或$\left\{{\begin{array}{l}{a=4}\\{b=-11}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{a=-3}\\{b=-11}\end{array}}\right.$或$\left\{{\begin{array}{l}{a=4}\\{b=3}\end{array}}\right.$ |
| A. | (0,+∞) | B. | (-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$) | C. | (-$∞,-\frac{\sqrt{3}}{2}$) | D. | (-∞,0) |
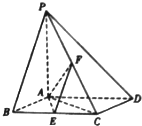 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.