题目内容
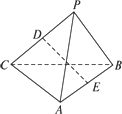
如图,P为平面ABCD外一点,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点,
(1)求证:PB⊥DM;
(2)求异面直线PB与CD所成角。
(1)求证:PB⊥DM;
(2)求异面直线PB与CD所成角。

(1)证明:∵N是PB的中点,M为PC中点,
∴MN∥BC,
∵BC∥AD,
∴MN∥AD,
∴A、D、M、N四点共面,
又∵PA=AB,
∴AN⊥PB,
又∵PA⊥面ABCD,PB在面ABCD内的射影为AB,
∵AD⊥AB,AD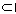 面ABCD,
面ABCD,
∴AD⊥PB,
又∵AN∩AD于A,
∴PB⊥面ADMN,
∴PB⊥MD;
(2)取AD中点H,连结BH、PH,
∵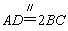 ,
,
∴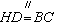 ,
,
∴BH∥CD,
∴∠PBH为异面直线CD与PB所成角或其补角,
设BC=1,则PA=AB=AD=2,则PB=2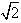 ,
,
在Rt△BAH中,BH=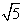 ,
,
在Rt△PAH中,PH=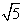 ,
,
∴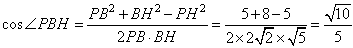 ,
,
即异面直线CD与PB所成角为 。
。
∴MN∥BC,
∵BC∥AD,
∴MN∥AD,
∴A、D、M、N四点共面,
又∵PA=AB,
∴AN⊥PB,
又∵PA⊥面ABCD,PB在面ABCD内的射影为AB,
∵AD⊥AB,AD
 面ABCD,
面ABCD, ∴AD⊥PB,
又∵AN∩AD于A,
∴PB⊥面ADMN,
∴PB⊥MD;
(2)取AD中点H,连结BH、PH,
∵
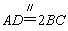 ,
, ∴
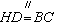 ,
, ∴BH∥CD,
∴∠PBH为异面直线CD与PB所成角或其补角,
设BC=1,则PA=AB=AD=2,则PB=2
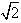 ,
,在Rt△BAH中,BH=
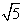 ,
,在Rt△PAH中,PH=
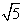 ,
,∴
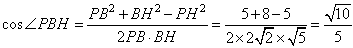 ,
,即异面直线CD与PB所成角为
 。
。 
练习册系列答案
相关题目
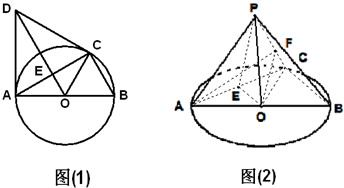 如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置,点P为平面ABC外的点.
如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置,点P为平面ABC外的点. (理)如图,P为△ABC所在平面外一点,且PA⊥平面ABC,∠ACB=90°,过点A作垂直于PC的截面ADE,截面交PC于点D,交PB于点E.
(理)如图,P为△ABC所在平面外一点,且PA⊥平面ABC,∠ACB=90°,过点A作垂直于PC的截面ADE,截面交PC于点D,交PB于点E.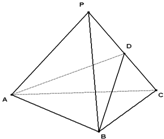 如图,P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC中点,直线PC与平面ABD垂直吗?为什么?
如图,P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC中点,直线PC与平面ABD垂直吗?为什么?