下列关于函数y=log2x的结论中正确的是②②．①与函数y=x2的图象关于y=x对称, ②图象恒过定点(1.0), ③图与直线y=-x无交点, ④定义域为[0.+∞)．题目和参考答案——青夏教育精英家教网—

题目内容

下列关于函数y=log₂x的结论中正确的是

②

．
①与函数y=x²的图象关于y=x对称； ②图象恒过定点（1，0）； ③图与直线y=-x无交点； ④定义域为[0，+∞）．

分析：结合对数函数的图象与性质即可得出正确选项：①与函数y=x²不是反函数，图象不关于y=x对称；②图象恒过定点（1，0）；③图与直线y=-x必有交点；④定义域为（0，+∞）．

解答：解：考察函数y=log₂x的图象与性质可知：
①与函数y=x²的图象不关于y=x对称；故错；
②图象恒过定点（1，0）；正确；
③图与直线y=-x必有交点；故错；
④定义域为（0，+∞）．故错．
故答案为：②

点评：本小题主要考查对数函数的图象与性质、对数函数的单调性与特殊点等基础知识，考查数形结合思想．属于基础题．

练习册系列答案

相关题目

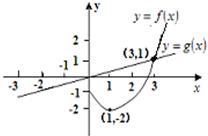对于任意的实数a，b，记max{a，b}=

a(a≥b)

b(a＜b)

．若F（x）=max{f（x），g（x）}（x∈R），其中函数 y=f（x）（x∈R）是奇函数，且当x≥0时，f（x）=（x-1）²-2；函数y=g（x）（x∈R）是正比例函数，其图象与x≥0时函数y=f（x）的图象如图所示，则下列关于函数y=F（x）的说法中，正确的是（　　）

A、y=F（x）为奇函数

B、y=F（x）在（-3，0）上为增函数

C、y=F（x）的最小值为-2，最大值为2

D、以上说法都不正确

（2012•道里区三模）已知函数f(x)=

kx+1，x≤0

lnx，x＞0

，则下列关于函数y=f[f（x）]+1的零点个数的判断正确的是（　　）

A．当k＞0时，有3个零点；当k＜0时，有2个零点

B．当k＞0时，有4个零点；当k＜0时，有1个零点

C．无论k为何值，均有2个零点

D．无论k为何值，均有4个零点

对于任意的实数a、b，记max{a，b}=

a(a≥b)

b(a＜b)

．若F（x）=max{f（x），g（x）}（x∈R），其中函数y=f（x）（x∈R）是奇函数，且在x=1处取得极小值-2，函数y=g（x）（x∈R）是正比例函数，其图象与x≥0时的函数y=f（x）的图象如图所示，则下列关于函数y=F（x）的说法中，正确的是（　　）

A．y=F（x）为奇函数

B．y=F（x）有极大值F（-1）

C．y=F（x）的最小值为-2，最大值为2

D．y=F（x）在（-3，0）上为增函数

下列关于函数y=log₂x的结论中，正确的是（　　）

对于任意的实数a、b，记max{a，b}=

a(a≥b)

b(a＜b)

．设F（x）=max{f（x），g（x）}（x∈R），其中g（x）=

x，y=f（x）是奇函数．当x≥0时，y=f（x）的图象与g（x）的图象如图所示．则下列关于函数y=F（x）的说法中，正确的是（　　）

A．y=F（x）有极大值F（-1）且无最小值

B．y=F（x）为奇函数

C．y=F（x）的最小值为-2且最大值为2

D．y=F（x）在（-3，0）上为增函数

试题分类