题目内容
如图，已知AD=5，DC=3，BC=4，将直角梯形ABCD绕AB边所在的直线旋转一周，由此形成的几何体的体积为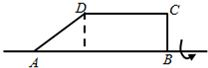
分析：由圆锥及圆柱的几何特征可得，该几何体由两个底面相待的圆锥和圆柱组合而成，其中圆柱和圆锥的高均为 3，代入圆柱和圆锥的体积公式，即可得到答案．
解答：解：如图，作DE⊥AB，则由已知，
得 DE=4，AE=3，
所以，形成的几何体的体积为
V=
π×42×3+π×42×3=64π．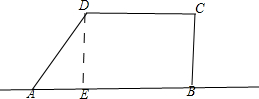
故答案为：64π．
得 DE=4，AE=3，
所以，形成的几何体的体积为
V=
| 1 |
| 3 |
故答案为：64π．
点评：本题考查的知识点是圆柱与圆锥的体积及余弦定理，关键是：（1）熟练掌握圆柱和圆锥的体积公式是关键，（2）将空间问题转化为平面问题是解答立体几何常用的技巧．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
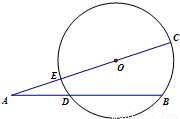
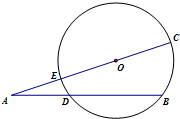（2013•通州区一模）如图，已知AD=5，DB=8，AO=3
（2012•湖北模拟）某校高二年级共有学生1000名，其中走读生750名，住宿生250名，现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查，根据问卷取得了这n名同学每天晚上有效学习时间（单位：分钟）的数据，按照以下区间分为八组：[0，30），[30，60），[60，90），[90，120），[120，150），[150，180），[180，210），[210.240），得到频率分布直方图如图，已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人．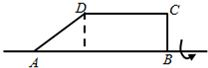
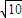，则圆O的半径OC的长为 ．