题目内容
某单位开展岗前培训.期间,甲、乙2人参加了5次考试,成绩统计如下:| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 甲的成绩 | 82 | 82 | 79 | 95 | 87 |
| 乙的成绩 | 95 | 75 | 80 | 90 | 85 |
(Ⅱ)根据有关概率知识,解答以下问题:
①从甲、乙2人的成绩中各随机抽取一个,设抽到甲的成绩为x,抽到乙的成绩为y.用A表示满足条件|x-y|≤2的事件,求事件A的概率;
②若一次考试两人成绩之差的绝对值不超过3分,则称该次考试两人“水平相当”.由上述5次成绩统计,任意抽查两次考试,求至少有一次考试两人“水平相当”的概率.
【答案】分析:(Ⅰ)先求出甲和乙的平均成绩相同,再求出甲和乙的成绩的方差,方差较小的发挥比较稳定,应该派他去.
(Ⅱ)①设抽到甲的成绩为x,抽到乙的成绩为y,则所有的(x,y)共有5×5=25个,用列举法求得满足条件|x-y|≤2的有5个,由此求得所求事件的概率.
②从5此考试的成绩中,任意取出2此,所有的基本事件有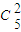 =10个,用列举法求得满足条件至少有一次考试两人“水平相当”的有7个,由此求得所求事件的概率.
=10个,用列举法求得满足条件至少有一次考试两人“水平相当”的有7个,由此求得所求事件的概率.
解答:解:(Ⅰ)甲的平均成绩为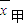 =
=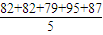 =85,乙的平均成绩为
=85,乙的平均成绩为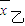 =
= =85,
=85,
故甲乙二人的平均水平一样.
甲的成绩的方差为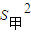 =
=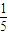
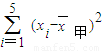 =31,乙的成绩的方差为
=31,乙的成绩的方差为 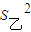 =
=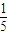
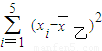 =50,∴
=50,∴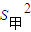 <
< ,故应派甲合适.
,故应派甲合适.
(Ⅱ)①从甲、乙2人的成绩中各随机抽取一个,设抽到甲的成绩为x,抽到乙的成绩为y,则所有的(x,y)共有5×5=25个,
其中,满足条件|x-y|≤2的有(82,80)、(82,80)、(79,80)、(95,95)、(87,85),共有5个,
故所求事件的概率等于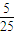 =
=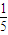 .
.
②从5此考试的成绩中,任意取出2此,所有的基本事件有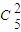 =10个,
=10个,
其中,满足至少有一次考试两人“水平相当”的有7个:(79,80)和(87,85)、(79,80)和(82,95)、(79,80)和(87,75)、
(79,80)和(95,90)、(87,85)和(82,95)、(87,85)和(82,75)、(87,85)和(95,90),共有7个,
故所求事件的概率等于 .
.
点评:本题考查古典概型及其概率计算公式的应用,应用列举法来解题是这一部分的最主要思想,平均数和方差的应用,属于基础题.
(Ⅱ)①设抽到甲的成绩为x,抽到乙的成绩为y,则所有的(x,y)共有5×5=25个,用列举法求得满足条件|x-y|≤2的有5个,由此求得所求事件的概率.
②从5此考试的成绩中,任意取出2此,所有的基本事件有
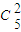 =10个,用列举法求得满足条件至少有一次考试两人“水平相当”的有7个,由此求得所求事件的概率.
=10个,用列举法求得满足条件至少有一次考试两人“水平相当”的有7个,由此求得所求事件的概率.解答:解:(Ⅰ)甲的平均成绩为
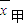 =
=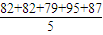 =85,乙的平均成绩为
=85,乙的平均成绩为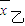 =
= =85,
=85,故甲乙二人的平均水平一样.
甲的成绩的方差为
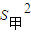 =
=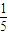
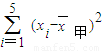 =31,乙的成绩的方差为
=31,乙的成绩的方差为 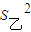 =
=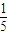
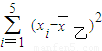 =50,∴
=50,∴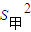 <
< ,故应派甲合适.
,故应派甲合适.(Ⅱ)①从甲、乙2人的成绩中各随机抽取一个,设抽到甲的成绩为x,抽到乙的成绩为y,则所有的(x,y)共有5×5=25个,
其中,满足条件|x-y|≤2的有(82,80)、(82,80)、(79,80)、(95,95)、(87,85),共有5个,
故所求事件的概率等于
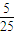 =
=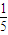 .
.②从5此考试的成绩中,任意取出2此,所有的基本事件有
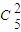 =10个,
=10个,其中,满足至少有一次考试两人“水平相当”的有7个:(79,80)和(87,85)、(79,80)和(82,95)、(79,80)和(87,75)、
(79,80)和(95,90)、(87,85)和(82,95)、(87,85)和(82,75)、(87,85)和(95,90),共有7个,
故所求事件的概率等于
 .
.点评:本题考查古典概型及其概率计算公式的应用,应用列举法来解题是这一部分的最主要思想,平均数和方差的应用,属于基础题.

练习册系列答案
相关题目
某单位开展岗前培训.期间,甲、乙2人参加了5次考试,成绩统计如下:
(Ⅰ)根据有关统计知识,回答问题:若从甲、乙2人中选出1人上岗,你认为选谁合适,请说明理由;
(Ⅱ)根据有关概率知识,解答以下问题:
①从甲、乙2人的成绩中各随机抽取一个,设抽到甲的成绩为x,抽到乙的成绩为y.用A表示满足条件|x-y|≤2的事件,求事件A的概率;
②若一次考试两人成绩之差的绝对值不超过3分,则称该次考试两人“水平相当”.由上述5次成绩统计,任意抽查两次考试,求至少有一次考试两人“水平相当”的概率.
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 甲的成绩 | 82 | 82 | 79 | 95 | 87 |
| 乙的成绩 | 95 | 75 | 80 | 90 | 85 |
(Ⅱ)根据有关概率知识,解答以下问题:
①从甲、乙2人的成绩中各随机抽取一个,设抽到甲的成绩为x,抽到乙的成绩为y.用A表示满足条件|x-y|≤2的事件,求事件A的概率;
②若一次考试两人成绩之差的绝对值不超过3分,则称该次考试两人“水平相当”.由上述5次成绩统计,任意抽查两次考试,求至少有一次考试两人“水平相当”的概率.