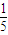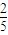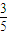题目内容
设P为△ABC所在平面内一点,且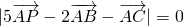 ,则△PAB的面积与△ABC的面积之比是
,则△PAB的面积与△ABC的面积之比是
- A.

- B.

- C.

- D.

A
分析:根据已知中,P为△ABC所在平面内一点,且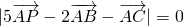 ,我们易得到
,我们易得到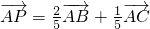 ,将AB延长至D,使长度AD=2AB,根据向量加法的平行四边形法则,我们易判断出P点在P点到AB边的距离为C点到AB边距离的
,将AB延长至D,使长度AD=2AB,根据向量加法的平行四边形法则,我们易判断出P点在P点到AB边的距离为C点到AB边距离的 ,进而得到△PAB的面积与△ABC的面积之比.
,进而得到△PAB的面积与△ABC的面积之比.
解答:∵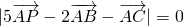
∴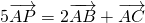
则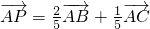
将AB延长至D,使长度AD=2AB
向量AD=2AB,则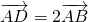
则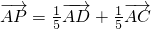
则
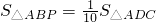
△PAB的面积与△ABC的面积之比是1:5
故选A
点评:本题考查的知识点是向量的共线定理,其中将AB延长至D,使长度AD=2AB,然后根据平行四边形法则临到P点在P点到AB边的距离为C点到AB边距离的 ,是解答本题的关键.
,是解答本题的关键.
分析:根据已知中,P为△ABC所在平面内一点,且
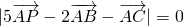 ,我们易得到
,我们易得到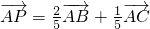 ,将AB延长至D,使长度AD=2AB,根据向量加法的平行四边形法则,我们易判断出P点在P点到AB边的距离为C点到AB边距离的
,将AB延长至D,使长度AD=2AB,根据向量加法的平行四边形法则,我们易判断出P点在P点到AB边的距离为C点到AB边距离的 ,进而得到△PAB的面积与△ABC的面积之比.
,进而得到△PAB的面积与△ABC的面积之比.解答:∵
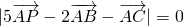
∴
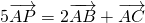
则
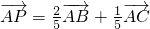
将AB延长至D,使长度AD=2AB
向量AD=2AB,则
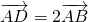
则
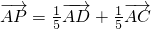
则

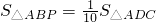
△PAB的面积与△ABC的面积之比是1:5
故选A
点评:本题考查的知识点是向量的共线定理,其中将AB延长至D,使长度AD=2AB,然后根据平行四边形法则临到P点在P点到AB边的距离为C点到AB边距离的
 ,是解答本题的关键.
,是解答本题的关键. 
练习册系列答案
相关题目
设P为△ABC所在平面内一点,且|5
-2
-
|=0,则△PAB的面积与△ABC的面积之比是( )
| AP |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
 ,则△PAB的面积与△ABC的面积之比是( )
,则△PAB的面积与△ABC的面积之比是( )



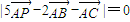 ,则△PAB的面积与△ABC的面积之比是( )
,则△PAB的面积与△ABC的面积之比是( )