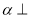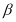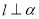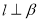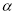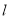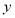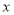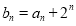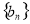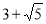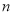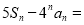题目内容
已知 为椭圆
为椭圆 ,
, 的左右焦点,
的左右焦点, 是坐标原点,过
是坐标原点,过 作垂直于
作垂直于 轴的直线
轴的直线 交椭圆于
交椭圆于 ,设
,设 .
.
(1)证明: 成等比数列;
成等比数列;
(2)若 的坐标为
的坐标为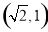 ,求椭圆
,求椭圆 的方程;
的方程;
(3)在(2)的椭圆中,过 的直线
的直线 与椭圆
与椭圆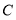 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.
(1)详见解析;(2)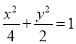 ;(3)
;(3)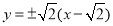
【解析】
试题分析:(1)由条件知M点的坐标为(c,y0),其中|y0|=d,知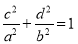 ,d=b•
,d=b•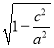 =
=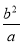 ,由此能证明d,b,a成等比数列;
,由此能证明d,b,a成等比数列;
(2)由条件知c=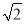 ,d=1,知b2=a?1,a2=b2+2,由此能求出椭圆方程;
,d=1,知b2=a?1,a2=b2+2,由此能求出椭圆方程;
(3)设点A(x1,y1)、B(x2,y2),当l⊥x轴时,A(-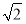 ,-1)、B(-
,-1)、B(-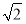 ,1),所以
,1),所以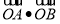 ≠0. 设直线
≠0. 设直线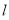 的方程为y=k(x+
的方程为y=k(x+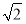 ),代入椭圆方程得(1+2k2)x2+4
),代入椭圆方程得(1+2k2)x2+4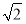 k2x+4k2?4=0再由韦达定理能够推导出直线
k2x+4k2?4=0再由韦达定理能够推导出直线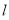 的方程.
的方程.
试题解析:(1)证明:由条件知M点的坐标为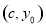 ,其中
,其中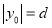 ,
,
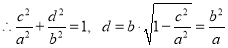 ,
, 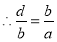 ,即
,即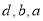 成等比数列. 3分
成等比数列. 3分
(2)由条件知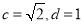 ,
,
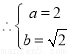
 椭圆方程为
椭圆方程为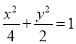 6分
6分
(3)设点A(x1,y1)、B(x2,y2),当l⊥x轴时,A(-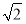 ,-1)、B(-
,-1)、B(-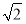 ,1),所以
,1),所以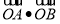 ≠0. 设直线
≠0. 设直线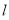 的方程为y=k(x+
的方程为y=k(x+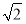 ),代入椭圆方程得(1+2k2)x2+4
),代入椭圆方程得(1+2k2)x2+4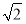 k2x+4k2?4=0所以
k2x+4k2?4=0所以 ①由
①由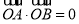 得
得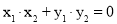
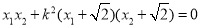 整理后把①式代入解得k=
整理后把①式代入解得k=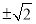 ,
,
所以直线l的方程为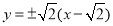 .
.
考点:数列与解析几何的综合.

练习册系列答案
相关题目