题目内容
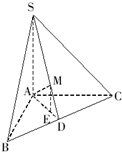 在三棱锥S-ABC中,SA⊥平面ABC,SA=AB=AC=
在三棱锥S-ABC中,SA⊥平面ABC,SA=AB=AC=
| ||
| 3 |
(1)求证:BC⊥AM;
(2)若AM⊥平面SBC,求证EM∥平面ABS.
分析:对(1),通过证明线面垂直⇒线线垂直即可;
对(2),将空间几何问题转化为平面几何问题,在△SAD中利用M、E分线段SD、AD成等比例,
证明ME与SA平行,再由线线平行⇒线面平行.
对(2),将空间几何问题转化为平面几何问题,在△SAD中利用M、E分线段SD、AD成等比例,
证明ME与SA平行,再由线线平行⇒线面平行.
解答:证明:(1)∵AB=AC,D是BC的中点,∴AD⊥BC,
∵SA⊥平面ABC,BC?平面ABC,∴SA⊥BC,SA∩AD=A,∴BC⊥平面SAD
∵AM?平面SAD,
∴BC⊥AM.
(2)∵AM⊥面SBC,SD?平面SBC⇒AM⊥SD,
∵SA=AB=AC=
BC,可设BC=3,SA=
在△ABC中,cos∠A=
=-
,∴∠A=
∴AD=
 .
.
在Rt△SAD中,
=2=
=
,∴SM=4MD,∵AE=4ED,
∴ME∥SA,ME?平面ABS,SA?平面ABS.
∴EM∥平面ABS.
∵SA⊥平面ABC,BC?平面ABC,∴SA⊥BC,SA∩AD=A,∴BC⊥平面SAD
∵AM?平面SAD,
∴BC⊥AM.
(2)∵AM⊥面SBC,SD?平面SBC⇒AM⊥SD,
∵SA=AB=AC=
| ||
| 3 |
| 3 |
在△ABC中,cos∠A=
| 3+3-9 | ||||
2×
|
| 1 |
| 2 |
| 2π |
| 3 |
| ||
| 2 |
 .
.在Rt△SAD中,
| SA |
| AD |
| AM |
| MD |
| SM |
| AM |

∴ME∥SA,ME?平面ABS,SA?平面ABS.
∴EM∥平面ABS.
点评:本题考查直线与平面平行、垂直的判定.利用平面几何知识证明线线平行是本题证明(II)的关键;另:将空间几何问题转化为平面几何问题是解决问题的常用方法.

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.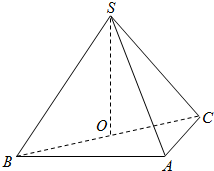 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C. 如图,在三棱锥S-ABC中,
如图,在三棱锥S-ABC中,