题目内容
2. 已知函数f(x)=Asin(ωx+φ).
已知函数f(x)=Asin(ωx+φ).(1)若该函数的部分图象如图所示,其中A>0,ω>0,0<φ<π,则该函数f(x)的解析式为f(x)=2sin(2x+$\frac{2π}{3}$)
(2)若A=2,ω=2,φ=0,则该函数图象在区间[-$\frac{π}{4}$,$\frac{3π}{4}$]上与直线y=-2围成封闭图形面积为π.
(3)若A=2,ω>2,φ=$\frac{π}{3}$,且该函数图象整体在区间[0,$\frac{π}{2}$]上有且只有4条对称轴,则ω取值集合为6≤ω<8.
分析 (1)由函数图象可得A,周期T,周期公式可求得ω,又点($\frac{\frac{π}{3}+\frac{π}{2}}{2}$,2)在函数图象上,可得:2sin(2×$\frac{\frac{π}{3}+\frac{π}{2}}{2}$+φ)=-2,结合范围0<φ<π,可得φ,从而可求函数解析式.
(2)由已知可得f(x)=2sin2x,数形结合,根据正弦函数的对称性可得,函数y=2sin2x的图象与函数y=-2的图象围成一个封闭图形可转化为以2及$\frac{π}{2}$为边长的矩形,从而可求面积.
(3)由已知可求f(x)=2sin(ωx+$\frac{π}{3}$).由函数f(x)=sin(ωx+$\frac{π}{3}$)图象在区间[0,$\frac{π}{2}$]上仅有4条对称轴,可得$\frac{3T}{2}≤\frac{π}{2}<2T$,利用周期公式即可得解.
解答 解:(1)由函数图象可得:A=2,又周期T=$\frac{5π}{6}$+($\frac{π}{2}$-$\frac{π}{3}$)=π,
由T=$π=\frac{2π}{ω}$,可解得:ω=2,
又点($\frac{\frac{π}{3}+\frac{π}{2}}{2}$,2)在函数图象上,可得:2sin(2×$\frac{\frac{π}{3}+\frac{π}{2}}{2}$+φ)=-2,
解得:φ=2kπ+$\frac{2π}{3}$,k∈Z,由0<φ<π,可得:φ=$\frac{2π}{3}$.
可得:f(x)=2sin(2x+$\frac{2π}{3}$).
(2)若A=2,ω=2,φ=0,则:f(x)=2sin2x.
数形结合,如图所示.
根据正弦函数的对称性可得,
曲线从x=-$\frac{π}{4}$到x=0与Y轴围成的面积与从x=0到x=$\frac{π}{4}$与Y轴围成的面积相等,
把x轴下方的阴影部分补到x轴上方,
∴函数y=2sin2x的图象与函数y=-2的图象围成一个封闭图形可转化为以2及$\frac{π}{2}$为边长的矩形.
所求的面积S=2×$\frac{π}{2}$=π.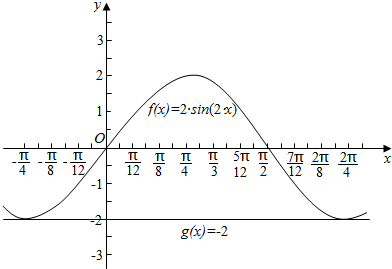
(3)若A=2,ω>2,φ=$\frac{π}{3}$,则:f(x)=2sin(ωx+$\frac{π}{3}$).
∴函数周期T=$\frac{2π}{ω}$,
∵函数f(x)=sin(ωx+$\frac{π}{3}$)图象在区间[0,$\frac{π}{2}$]上仅有4条对称轴,
∴$\frac{3T}{2}≤\frac{π}{2}<2T$,即可得:$\frac{3}{2}×\frac{2π}{ω}≤\frac{π}{2}<2×\frac{2π}{ω}$,解得:6≤ω<8.
故答案为:2sin(2x+$\frac{2π}{3}$),π,6≤ω<8.
点评 本题着重考查了正弦曲线的对称性和y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式等知识,考查几何图形的面积的求法,考查发现问题解决问题的能力,属于中档题.

