题目内容
我国西南地区正遭受着百年不遇的旱灾.据气象预报,未来48小时受灾最严重的甲地有望迎来一次弱降雨过程.某军区命令M部队立即前往甲地准备实施人工增雨作业,已知“人工增雨”高炮车Ⅰ号载有3枚“增雨炮弹”和1枚“增雨火箭”,通过炮击“积雨云”实施增雨,第一次击中积雨云只能使云层中的水分子凝聚,第二次击中同一积雨云才能成功增雨.如果需要,第4次射击才使用“增雨火箭”,当增雨成功或者增雨弹用完才停止射击.每次射击相互独立,且用“增雨炮弹”击中积雨云的概率是| 2 |
| 3 |
| 8 |
| 9 |
(Ⅰ)求不使用“增雨火箭”就能成功增雨的概率;
(Ⅱ)求要使用“增雨火箭”才能成功增雨的概率;
(Ⅲ)求射击次数不小于3的概率.
分析:对于(Ⅰ)求不使用“增雨火箭”就能成功增雨的概率,因为要2次击中才能增雨成功,故分为2种可能性,前2次增雨炮弹击中或前2次增雨火箭有一次没击中,第3次击中.求出它们的概率和即可得到答案.
(Ⅱ)求要使用“增雨火箭”才能成功增雨的概率,即前3次射击中有且只有一次击中积雨云,且第四次射击也要击中积雨云.求出概率即可.
(Ⅲ)求射击次数不小于3的概率,可以求其反面小于3次,故只能是2次,求出概率.用1减去它即可得到答案.
(Ⅱ)求要使用“增雨火箭”才能成功增雨的概率,即前3次射击中有且只有一次击中积雨云,且第四次射击也要击中积雨云.求出概率即可.
(Ⅲ)求射击次数不小于3的概率,可以求其反面小于3次,故只能是2次,求出概率.用1减去它即可得到答案.
解答:解:(I)设不使用“增雨火箭”就成功增雨的概率为P1,则
P1=
•
+
(1-
)•
•
=
.
(II)要使用“增雨火箭”才能成功增雨,就必须是前3次射击中有且只有一次击中积雨云,且第四次射击也要击中积雨云.设概率为P2,则P2=
(1-
)2•
•
=
.
(3)设射击次数不小于3次的概率为P3,则P3=1-
•(
)2=
.
P1=
| 2 |
| 3 |
| 2 |
| 3 |
| C | 1 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 20 |
| 27 |
(II)要使用“增雨火箭”才能成功增雨,就必须是前3次射击中有且只有一次击中积雨云,且第四次射击也要击中积雨云.设概率为P2,则P2=
| C | 1 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 9 |
| 16 |
| 81 |
(3)设射击次数不小于3次的概率为P3,则P3=1-
| C | 2 2 |
| 2 |
| 3 |
| 5 |
| 9 |
点评:此题主要考查n次独立重复试验中恰好发生k次的概率,其中涉及到相互独立事件的概率乘法公式的应用.在新课程的改革后,求这种实际应用的题目会增加,同学们需要注意.

练习册系列答案
相关题目
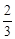 ,用“增雨火箭”击中积雨云的概率是
,用“增雨火箭”击中积雨云的概率是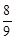 .
.
 ,用“增雨火箭”击中积雨云的概率是
,用“增雨火箭”击中积雨云的概率是 .
.