题目内容
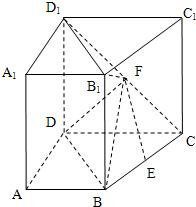 已知直四棱柱ABCD-A1B1C1D1,底面ABCD为直角梯形,AB∥CD,AB⊥AD,CD=DD1=4,AD=AB=2,E、F分别为BC、CD1中点.
已知直四棱柱ABCD-A1B1C1D1,底面ABCD为直角梯形,AB∥CD,AB⊥AD,CD=DD1=4,AD=AB=2,E、F分别为BC、CD1中点.(I)求证:EF∥平面BB1D1D;
(Ⅱ)求证:BC⊥平面BB1D1D;
(Ⅲ)求四棱锥F-BB1D1D的体积.
分析:(I)要证:EF∥平面BB1D1D,根据线面平行的判定定理可知:只需证EF∥BD1即可.
(Ⅱ)要证:BC⊥平面BB1D1D;根据线面垂直的判定定理可知:只需证:BC⊥BD的BC⊥BB1,即可.
(Ⅲ)要求四棱锥F-BB1D1D的体积.关键是求高,即找底面的垂线,由(Ⅱ)知BC⊥平面BB1D1D,∴FN⊥平面BB1D1D,则FN是四棱锥F-BB1D1D的高,再求得S四边形BB1D1D,最后由体积公式求解.
(Ⅱ)要证:BC⊥平面BB1D1D;根据线面垂直的判定定理可知:只需证:BC⊥BD的BC⊥BB1,即可.
(Ⅲ)要求四棱锥F-BB1D1D的体积.关键是求高,即找底面的垂线,由(Ⅱ)知BC⊥平面BB1D1D,∴FN⊥平面BB1D1D,则FN是四棱锥F-BB1D1D的高,再求得S四边形BB1D1D,最后由体积公式求解.
解答: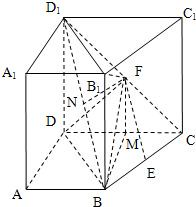 证明:
证明:
(I)连接BD1,∵E、F分别为BC、CD1中点;
∴EF∥BD1,(2分)
又∵BD1?平面BB1D1D,EF?平面BB1D1D
∴EF∥平面BB1D1D;(4分)(少一条件扣1分)
(Ⅱ)取CD中点M,连接BM,则DM=CM=2,
∵AB∥CD,AB⊥AD,
∴四边形ABMD是正方形,则DM=CM=BM=2,
∴BC⊥BD,(7分)(或由计算证明)
在直四棱柱ABCD-A1B1C1D1中,有BC⊥BB1,且BD∩BB1=B,
∴BC⊥平面BB1D1D;(9分)
(Ⅲ)取BD1中点N,连接FN,则FN∥BC,(10分)
由(Ⅱ)知BC⊥平面BB1D1D,∴FN⊥平面BB1D1D,
则FN是四棱锥F-BB1D1D的高,且FN=
BC=
∵S四边形BB1D1D=8
∴V=
(14分)
 证明:
证明:(I)连接BD1,∵E、F分别为BC、CD1中点;
∴EF∥BD1,(2分)
又∵BD1?平面BB1D1D,EF?平面BB1D1D
∴EF∥平面BB1D1D;(4分)(少一条件扣1分)
(Ⅱ)取CD中点M,连接BM,则DM=CM=2,
∵AB∥CD,AB⊥AD,
∴四边形ABMD是正方形,则DM=CM=BM=2,
∴BC⊥BD,(7分)(或由计算证明)
在直四棱柱ABCD-A1B1C1D1中,有BC⊥BB1,且BD∩BB1=B,
∴BC⊥平面BB1D1D;(9分)
(Ⅲ)取BD1中点N,连接FN,则FN∥BC,(10分)
由(Ⅱ)知BC⊥平面BB1D1D,∴FN⊥平面BB1D1D,
则FN是四棱锥F-BB1D1D的高,且FN=
| 1 |
| 2 |
| 2 |
∵S四边形BB1D1D=8
| 2 |
∴V=
| 16 |
| 3 |
点评:本题主要考查了线面平行的判定定理和线面垂直的判定定理,还考查了辅助线的作法和转化思想,属中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
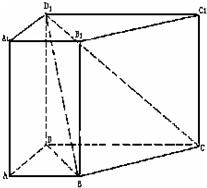 已知直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=AD=1,DD1=CD=2,AB⊥AD.
已知直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=AD=1,DD1=CD=2,AB⊥AD.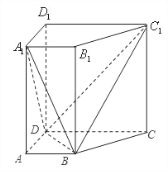 如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足
如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: 已知直四棱柱ABCD-A1B1C1D1的底面是菱形,F为棱BB1的中点,M为线段AC1的中点.
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,F为棱BB1的中点,M为线段AC1的中点. (2010•宝山区模拟)已知直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,且BC⊥AB.
(2010•宝山区模拟)已知直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,且BC⊥AB.