题目内容
(1)动直线y=a与抛物线y2=![]() (x-2)相交于A点,动点B的坐标是(0,3a),求线段AB中点M的轨迹C的方程;
(x-2)相交于A点,动点B的坐标是(0,3a),求线段AB中点M的轨迹C的方程;
(2)过点D(2,0)的直线l交上述轨迹C于P、Q两点,E点坐标是(1,0),若△EPQ的面积为4,求直线l的倾斜角α的值.
答案:
解析:
解析:
(1)解:设M点的坐标为(x,y),由点A的坐标为(2a2+2,a),B点的坐标为(0,3a),得 ∴轨迹C的方程为x= 即y2=4(x-1); (2)解法一:设直线l的方程为y=k(x-2),因l与抛物线有两个交点,故k≠0,得x= 故Δ= 记这个方程的两实根为y1、y2,则 |PQ|= 又点E到直线l的距离 d= ∴△EPQ的面积为S△EPQ= 由 ∴α= 解法二:设直线l的方程为y=k(x-2),代入y2=4(x-1),得 k2x2-(4k2+4)x+4k2+4=0. 因直线l与抛物线有两个交点,故k≠0, 而Δ=16(k2+1)>0恒成立. 记这个方程的两个实根为x1、x2,因抛物线y2=4(x-1)的焦点是D(2,0),准线是x=0. 所以|PQ|=x1+x2= 其余同解法一. 解法三:设直线l的方程为y=k(x-2),因为直线与抛物线交于两点,所以k≠0,则x= S△EPQ=S△EPD+S△EQD= = = ∵S△EPQ=4, ∴ 得k=± |

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
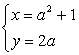 .
. .
.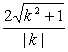 =4,解得k2=
=4,解得k2=