题目内容
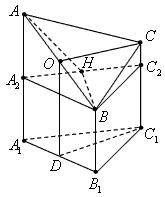
下图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC。已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,
(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)求AB与平面AA1C1C所成的角的大小;
(3)求此几何体的体积。
(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)求AB与平面AA1C1C所成的角的大小;
(3)求此几何体的体积。

解:(1)作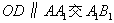 于D,连接 于D,连接 , ,则 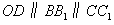 , ,因为O是AB的中点, 所以 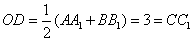 , ,则 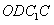 是平行四边形,因此有 是平行四边形,因此有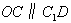 , ,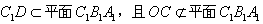 , ,则OC∥面 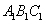 。 。(2)如图,过B作截面 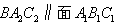 , ,分别交 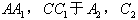 , ,作  于H, 于H,因为平面 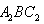 ⊥平面 ⊥平面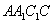 ,则BH⊥面 ,则BH⊥面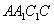 , ,连结AH,则∠BAH就是AB与面 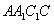 所成的角. 所成的角.因为 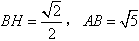 ,所以 ,所以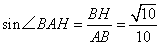 , ,AB与面 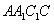 所成的角为 所成的角为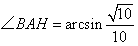 。 。(3)因为 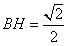 , ,所以 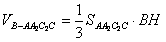 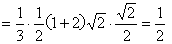 , ,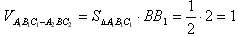 , ,所求几何体的体积为 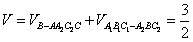 。 。 |
 |

练习册系列答案
相关题目



