题目内容
如图1-1-8,在四边形ABCD中,BC=m,DC=2m,四个内角A、B、C、D之比为3∶7∶4∶10,试求四边形ABCD的面积

图1-1-8
思路分析:四边形的基本构成元素是三角形,因而可把该问题转化为求三角形面积,首先可根据四个内角的度数之比求出四个内角,结合余弦定理求得边长,利用三角形面积公式S=![]() absinC求解.
absinC求解.
解:由题意知,设四个内角A、B、C、D的大小依次为3x、7x、4x、10x,则3x+7x+4x+10x=360°.
∴x=15°,即A=45°,B=105°,C=60°,D=150°.
在△BCD中,由余弦定理,得
BD2=BC2+DC2-2BC·DC·cosC=m2+(2m)2-2×m×2m×cos60°=3m2.
∴BD=3m.
∴S△BCD=![]() DC·BC·sinC=
DC·BC·sinC=![]() ×m×2m×
×m×2m×![]() =
=![]() m2.
m2.
在△BCD中,BD2+BC2=DC2,∴∠DBC=90°.∴∠BDC=30°.
在△BAD中,由正弦定理,得
AB=![]() =
=![]() =
=![]() m.
m.
又∠ABD=105°-90°=15°,
∴S△ABD=![]() AB·BD·sin15°=
AB·BD·sin15°=![]() ×
×![]() m×
m×![]() m×
m×![]() =
=![]() m2.
m2.
∴S四边形ABCD=S△BCD+S△ABD=![]() m2+
m2+![]() m2=
m2=![]() m2.
m2.

练习册系列答案
相关题目
 如图茎叶图记录了甲、乙两组四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中以X表示.
如图茎叶图记录了甲、乙两组四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中以X表示.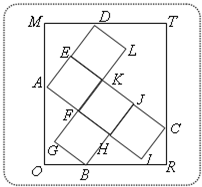 如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上.
如图,已知矩形ORTM内有5个全等的小正方形,其中顶点A、B、C、D在矩形ORTM的四条边上. ,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为 (假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路 (如图(1)所示,其中
(如图(1)所示,其中 (
( )),且前轮
)),且前轮 已在
已在 段上时,后轮中心在
段上时,后轮中心在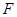 位置;若前轮中心到达
位置;若前轮中心到达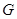 处时,后轮中心在
处时,后轮中心在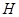 处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
处(假定该汽车能顺利驶上该上坡路). 设前轮中心在 和
和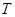 ,且
,且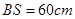 ,
,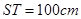 . (其它因素忽略不计)
. (其它因素忽略不计)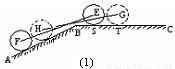
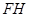 和
和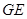 的延长线交于点
的延长线交于点 ,
,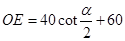 (cm);
(cm);
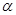 =
=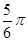 时,后轮中心从
时,后轮中心从 中,
中, ,
, ,
, ,
, ,
, 分别是
分别是 的中点,现将
的中点,现将 沿
沿 折起,使平面
折起,使平面 平面
平面 (如图2),且所得到的四棱锥
(如图2),且所得到的四棱锥 的正视图、侧视图、俯视图的面积总和为8.
的正视图、侧视图、俯视图的面积总和为8. 到平面
到平面 的距离;
的距离; 的大小的夹角的余弦值;
的大小的夹角的余弦值; 上确定一点
上确定一点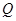 ,使
,使 平面
平面 ,并给出证明过程.
,并给出证明过程.