题目内容
当n为正整数时,定义函数N (n)表示n的最大奇因数.如N (3)=3,N (10)=5,….记S(n)=N(1)+N(2)+N(3)+…+N(2n).则(1)S(4)=
.
86
86
.(2)S(n)=| 4n+2 | 3 |
分析:(1)由题设知,N(2n)=N(n),N(2n-1)=2n-1.S(4)=[N(1)+N(3)+N(5)+…+N(15)]+[N(2)+N(4)+N(6)+…+N(16)]=[1+3+5+…+15]+[N(2)+N(4)+N(6)+…+N(16)].由此能求出S(4).
(2)由S(n)=[1+3+5+…+(2n-1)]+[N(2)+N(4)+N(6)+…+N(2n)],知S(n)=4n-1+S(n-1)(n≥1),由此能推导出S(n)=4n-1+4n-2+…+41+40+1=
.
(2)由S(n)=[1+3+5+…+(2n-1)]+[N(2)+N(4)+N(6)+…+N(2n)],知S(n)=4n-1+S(n-1)(n≥1),由此能推导出S(n)=4n-1+4n-2+…+41+40+1=
| 4n+2 |
| 3 |
解答:解:(1)由题设知,N(2n)=N(n),N(2n-1)=2n-1.
S(4)=[N(1)+N(3)+N(5)+…+N(15)]+[N(2)+N(4)+N(6)+…+N(16)]
=[1+3+5+…+15]+[N(2)+N(4)+N(6)+…+N(16)]
=43+S(3)
=43+42+S(2)
=43+42+41+S(1)=86.
(2)S(n)=[1+3+5+…+(2n-1)]+[N(2)+N(4)+N(6)+…+N(2n)],
∴S(n)=4n-1+S(n-1)(n≥1),
又S1=N(1)=1,
∴S(n)=4n-1+4n-2+…+41+40+1=
.
S(4)=[N(1)+N(3)+N(5)+…+N(15)]+[N(2)+N(4)+N(6)+…+N(16)]
=[1+3+5+…+15]+[N(2)+N(4)+N(6)+…+N(16)]
=43+S(3)
=43+42+S(2)
=43+42+41+S(1)=86.
(2)S(n)=[1+3+5+…+(2n-1)]+[N(2)+N(4)+N(6)+…+N(2n)],
∴S(n)=4n-1+S(n-1)(n≥1),
又S1=N(1)=1,
∴S(n)=4n-1+4n-2+…+41+40+1=
| 4n+2 |
| 3 |
点评:本题考查等比数列的性质和应用,解题时要注意等比当选列的前n项和公式、通项公式的灵活运用,注意总结规律,认真解答.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

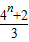 .
.