题目内容
(本小题满分12分)
矩形ABCD的对角线AC、BD相交于点M (2,0),AB边所在直线的方程为: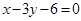 ,若点
,若点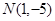 在直线AD上.
在直线AD上.
(1)求点A的坐标及矩形ABCD外接圆的方程;
(2)过点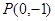 的直线
的直线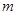 与ABCD外接圆相交于A、B两点,若
与ABCD外接圆相交于A、B两点,若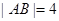 ,求直线m的方程.
,求直线m的方程.
(1) 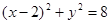 ;(2)
;(2)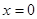 或
或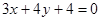 。
。
解析试题分析:(1)∵AC⊥AD 且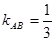 ∴
∴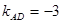
∴直线AD的方程为: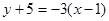 即
即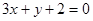 ………2分
………2分
由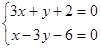 解得
解得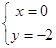 即A(0,-2) ………4分
即A(0,-2) ………4分
∵ABCD是矩形 ∴ABCD外接圆的圆心为对角线AC与BD的交点,即M(2,0),
半径r="|AM|=2" 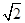 . 故其方程为
. 故其方程为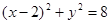 ………6分
………6分
(2)①当直线m的斜率不存在时,其方程为x="0," m与圆M的交点为A(0,-2),B(0,2)
满足|AB|=4, ∴x=0符合题意。 ………8分
②当直线m的斜率存在时,设m的方程为y=kx-1,即kx-y-1=0,则圆心(2,0)到直线m的距离为: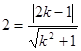 解得:
解得: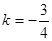
∴此时m的方程为: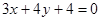
故所求m的方程为: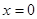 或
或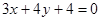 ………12分
………12分
考点:本题主要考查直线方程,圆的方程,直线与圆的位置关系。
点评:典型题,涉及求圆的问题,往往利用定义法—即求圆心、半径,或利用“待定系数法”。本题中求切线方程是一道易错题,应该注意到,自圆外一点作圆的切线有两条,防止遗漏“斜率”不存在的切线。

练习册系列答案
相关题目
 中,已知圆
中,已知圆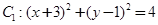 和圆
和圆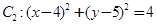 .
. 过点
过点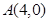 ,且被圆
,且被圆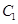 截得的弦长为
截得的弦长为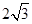 ,求直线
,求直线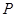 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点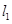 和
和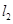 ,它们分别与圆
,它们分别与圆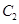 相交,且直线
相交,且直线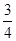 ,且与坐标轴所围成的三角形的周长是12的直线的方程。
,且与坐标轴所围成的三角形的周长是12的直线的方程。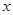 O
O 中,直线
中,直线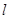 与抛物线
与抛物线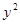 =2
=2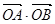 =3”是真命题;
=3”是真命题;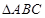 的顶点
的顶点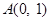 ,
,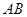 边上的中线
边上的中线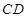 所在的直线方程为
所在的直线方程为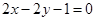 ,
,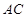 边上的高
边上的高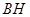 所在直线的方程为
所在直线的方程为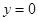 。
。 、
、 的坐标;
的坐标; 经过不同的三点
经过不同的三点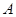 、
、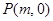 ,且斜率为
,且斜率为 的直线与圆
的直线与圆 ,求圆
,求圆 ,使
,使 ,以
,以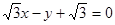 与
与 轴,
轴,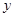 轴分别相交于A、B两点,以AB为边做等边
轴分别相交于A、B两点,以AB为边做等边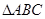 ,若平面内有一点
,若平面内有一点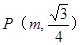 使得
使得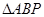 与
与 的值.
的值. 的图象与
的图象与 轴分别相交于点
轴分别相交于点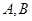 两点,向量
两点,向量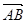
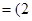 ,
,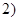 ,又函数
,又函数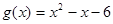 ,且
,且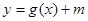 的值域是
的值域是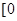 ,
,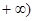 。
。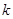 ,
, 及
及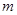 的值;(2)当
的值;(2)当 满足
满足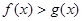 时,求函数
时,求函数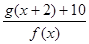 的最小值。
的最小值。 ,求函数
,求函数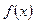 图象上的点到
图象上的点到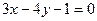 距离的最小值,并求出相应的点的坐标.
距离的最小值,并求出相应的点的坐标.