题目内容
已知数列{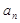 }的前
}的前 项和为
项和为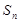 ,且满足
,且满足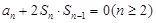 ,
,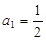 .
.
(1)求证:{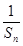 }是等差数列;
}是等差数列;
(2)求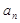 表达式;
表达式;
(3)若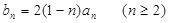 ,求证:
,求证: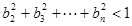 .
.
(1)见解析 (2)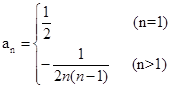 (3)见解析
(3)见解析
解析试题分析:(1)利用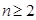 时,
时,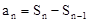 ,将
,将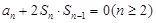 ,变形为
,变形为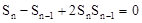 S进而得到
S进而得到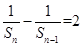 ,又
,又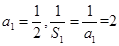 ,即可得证
,即可得证
(2)由(1),利用等差数列的通项公式即可的到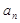
(3)由(2)知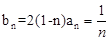 ,则
,则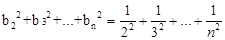 ,到这里,首先利用放缩法,然后再利用裂项相消法即可
,到这里,首先利用放缩法,然后再利用裂项相消法即可
(1)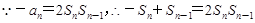
 ,∴
,∴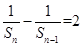 ,又
,又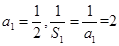
∴{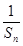 }是以2为首项,公差为2的等差数列.
}是以2为首项,公差为2的等差数列.
(2)由(1)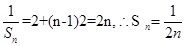
当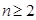 时,
时,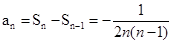 an=Sn-Sn-1=-
an=Sn-Sn-1=-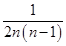
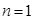 时,
时,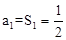 ,
,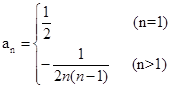
(3)由(2)知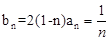
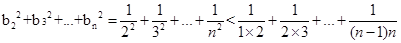
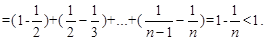
考点:等差数列,裂项相消法

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 ,b1 = 3,求数列
,b1 = 3,求数列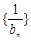 的前n项和Tn.
的前n项和Tn. 是等差数列,其中
是等差数列,其中 ,前四项和
,前四项和 .
. ,①求数列
,①求数列 的前
的前 项之和
项之和
 是不是数列
是不是数列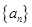 的前
的前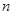 项和
项和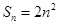 ,
,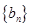 为等比数列,且
为等比数列,且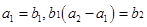 .
.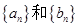 的通项公式;(2)设
的通项公式;(2)设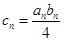 ,求数列
,求数列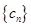 前
前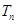 .
.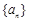 的公差
的公差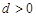 ,设
,设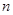 项和为
项和为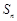 ,
,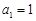 ,
,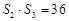
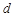 及
及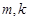 (
(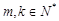 )的值,使得
)的值,使得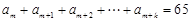 .
.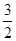 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.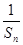 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.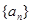 的前
的前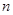 项和为
项和为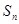 且
且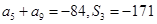 .
.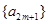 的前
的前 项和
项和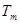 ,并求
,并求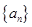 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项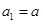 ,
,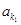 、
、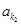 、…、
、…、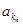 恰为等比数列,且
恰为等比数列,且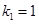 ,
,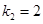 ,
,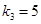 .
. (用
(用 表示);
表示); 的前
的前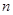 项和为
项和为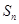 ,求
,求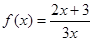 , 数列
, 数列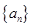 满足
满足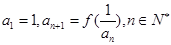 .
.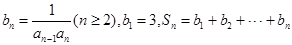 ,若
,若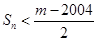 对一切
对一切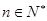 成立,求最小正整数m.
成立,求最小正整数m.