题目内容
一只球放在桌面上,桌面上一点A的正上方有一点光源O,OA与球相切,让A在桌面上运动,OA始终与球相切,OA形成一个轴截面顶角为45°的圆锥,则点A的轨迹椭圆的离心率为 .
【答案】分析:根据圆曲线的第一定义,作出过圆锥的轴与椭圆长轴AA′的截面,可得等腰直角三角形AOA′,在此三角形中利用切线长定理,可以求出焦点到长轴顶点距离AF与AA′的关系式,再根据椭圆的几何性质,化为关于椭圆的参数a、c的等量关系,即可求出椭圆的离心率.
解答:解: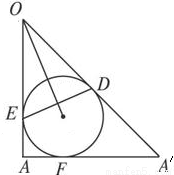 如图是过圆锥的轴与椭圆长轴AA′的截面,根据圆锥曲线的定义,
如图是过圆锥的轴与椭圆长轴AA′的截面,根据圆锥曲线的定义,
可得球与长轴AA′的切点是椭圆的焦点F,OA⊥AA′
设光线OA与球相切于点E,OA′与球相切于点D
∵等腰直角三角形AOA′中,OA=AA′=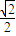 OA/
OA/
∴AF=AE= (OA+AA′-OA′)=AA′-
(OA+AA′-OA′)=AA′-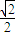 AA′=(1-
AA′=(1-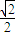 )AA′
)AA′
根据椭圆的几何性质,得长轴AA′=2a,
AF是焦点到长轴顶点的距离AF=a-c
代入到上式,得a-c=(1-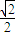 )•2a⇒
)•2a⇒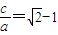
所以所求椭圆的离心率为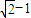
故答案为: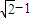
点评:本题以空间的圆锥为载体,考查了圆锥曲线的形成过程,同时考查了椭圆的基本量,属于中档题.深刻理解空间位置关系和椭圆的定义与性质,是解决本题的关键.
解答:解:
 如图是过圆锥的轴与椭圆长轴AA′的截面,根据圆锥曲线的定义,
如图是过圆锥的轴与椭圆长轴AA′的截面,根据圆锥曲线的定义,可得球与长轴AA′的切点是椭圆的焦点F,OA⊥AA′
设光线OA与球相切于点E,OA′与球相切于点D
∵等腰直角三角形AOA′中,OA=AA′=
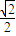 OA/
OA/∴AF=AE=
 (OA+AA′-OA′)=AA′-
(OA+AA′-OA′)=AA′-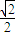 AA′=(1-
AA′=(1-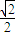 )AA′
)AA′根据椭圆的几何性质,得长轴AA′=2a,
AF是焦点到长轴顶点的距离AF=a-c
代入到上式,得a-c=(1-
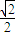 )•2a⇒
)•2a⇒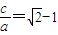
所以所求椭圆的离心率为
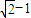
故答案为:
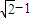
点评:本题以空间的圆锥为载体,考查了圆锥曲线的形成过程,同时考查了椭圆的基本量,属于中档题.深刻理解空间位置关系和椭圆的定义与性质,是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目