Question

一只球放在桌面上，桌面上一点A的正上方有一点光源O，OA与球相切，让A在桌面上运动，OA始终与球相切，OA形成一个轴截面顶角为45°的圆锥，则点A的轨迹椭圆的离心率为______．

Answer 1

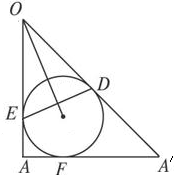
如图是过圆锥的轴与椭圆长轴AA′的截面，根据圆锥曲线的定义，
可得球与长轴AA′的切点是椭圆的焦点F，OA⊥AA′
设光线OA与球相切于点E，OA′与球相切于点D
∵等腰直角三角形AOA′中，OA=AA′=

2

2

OA^/
∴AF=AE=

1

2

（OA+AA′-OA′）=AA′-

2

2

AA′=（1-

2

2

）AA′
根据椭圆的几何性质，得长轴AA′=2a，
AF是焦点到长轴顶点的距离AF=a-c
代入到上式，得a-c=（1-

2

2

）•2a?

c

a

=

2

-1
所以所求椭圆的离心率为

2

-1
故答案为：

2

-1