题目内容
在△ABC中,内角 所对的边分别是
所对的边分别是 .若
.若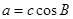 ,则△ABC是
,则△ABC是
| A.等腰三角形 | B.等边三角形 | C.直角三角形 | D.等腰直角三角形 |
C
解析试题分析:因为对于三角形形状的判定要不就通过角,要不就通过边,那么可以利用正弦定理进行边角转化,由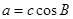 ,
, 得到sinA2R=sinC2RcosB.化简得到为sinA=cosBsinC=sin(B+C)=sinBcosC+cosBsinC,这样可得到sinBcosC=0,而因为sinB>0,故cosC=0,则说明C为直角,因此该三角形为直角三角形,选C.
得到sinA2R=sinC2RcosB.化简得到为sinA=cosBsinC=sin(B+C)=sinBcosC+cosBsinC,这样可得到sinBcosC=0,而因为sinB>0,故cosC=0,则说明C为直角,因此该三角形为直角三角形,选C.
考点:本试题主要考查了正弦定理、两角和差的三角公式和三角形的内角和定理的综合运用,
点评:解决该试题的关键是对于边化角后,能运用内角和定理中sinA=sin(C+B),化简变形得到结论。

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知 中,
中,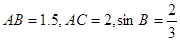 .则
.则 ( )。
( )。
A. | B. | C. 或 或 | D. 或 或 |
在△ 中,内角
中,内角 的对边分别为
的对边分别为 。若
。若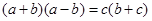 ,则
,则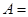
A.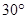 | B.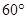 | C.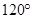 | D.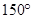 |
某人要制作一个三角形,要求它的三条高的长度分别为 则此人能( )
则此人能( )
| A.不能作出这样的三角形. | B.作出一个锐角三角形. |
| C.作出一个直角三角形. | D.作出一个钝角三角形. |
在△ 中,若
中,若 ,则△
,则△ 的形状是( )
的形状是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不能确定 |
在 中,如果
中,如果 ,那么角
,那么角 等于 ( )
等于 ( )
A. | B. | C. | D. |
若(a+b+c)(b+c-a)=3bc,且sinA="2sinBcosC," 那么ΔABC是( )
| A.直角三角形 | B.等腰直角三角形 |
| C.等腰三角形 | D.等边三角形 |
 与两灯塔A、B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30
与两灯塔A、B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30 ,灯塔B在观察站C正西方向,则两灯塔A、B间的距离为
,灯塔B在观察站C正西方向,则两灯塔A、B间的距离为  ,那么△ABC是( ).
,那么△ABC是( ).