题目内容
已知点F(0，1)，直线l：y=-l，P为平面上的动点，过点P作直线l的垂线，垂足为Q，且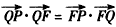
，
(Ⅰ)求动点P的轨迹C的方程；
(Ⅱ)已知圆M过定点D(0，2)，圆心M在轨迹C上运动，且圆M与x轴交于A，B两点，设|DA|=l1，|DB|=l2，求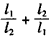
的最大值。
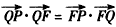，(Ⅰ)求动点P的轨迹C的方程；
(Ⅱ)已知圆M过定点D(0，2)，圆心M在轨迹C上运动，且圆M与x轴交于A，B两点，设|DA|=l1，|DB|=l2，求
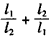的最大值。解：(Ⅰ)设P（x，y），则Q（x，-1），
∵
，
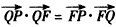∴ (0，y+l)·(-x，2)=(x，y-1)·(x，-2)，
即2(y+1)=x2-2(y-1)，即x2=4y，
所以动点P的轨迹C的方程x2=4y。
(Ⅱ)设圆M的圆心坐标为M(a，b)，则a2=4b ①，
圆M的半径为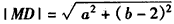
，
圆M的方程为(x-a)2+(y-b)2=a2+(b-2)2，
令y=0，则(x-a)2+b2=a2+(b-2)2，
整理得，x2-2ax+4b-4=0， ②
由①，②解得：x=a±2，
不妨设A（a-2，0），B（a+2，0），
∴
，
∴
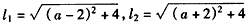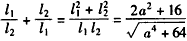
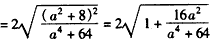， ③
当a≠0时，由③得
，
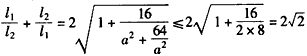当且仅当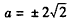
时，等号成立，
当a=0时，由③，得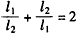
；
当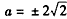
时，
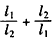的最大值为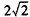
。
∵
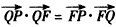，∴ (0，y+l)·(-x，2)=(x，y-1)·(x，-2)，
即2(y+1)=x2-2(y-1)，即x2=4y，
所以动点P的轨迹C的方程x2=4y。
(Ⅱ)设圆M的圆心坐标为M(a，b)，则a2=4b ①，
圆M的半径为
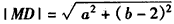，圆M的方程为(x-a)2+(y-b)2=a2+(b-2)2，
令y=0，则(x-a)2+b2=a2+(b-2)2，
整理得，x2-2ax+4b-4=0， ②
由①，②解得：x=a±2，
不妨设A（a-2，0），B（a+2，0），
∴
，∴
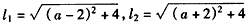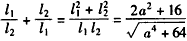
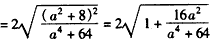， ③当a≠0时，由③得
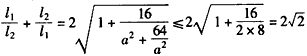，当且仅当
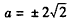时，等号成立，当a=0时，由③，得
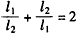；当
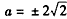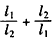时，的最大值为。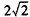
练习册系列答案
相关题目
(1)求点P的轨迹方程；
？若存在，求出λ的值，若不存在，请说明理由．
，动点P的轨迹为C，已知圆M过定点D(0，2)，圆心M在轨迹C上运动，且圆M与x轴交于A、B两点，设|DA|＝l1，|DB|＝l2，则
的最大值为
．
的最大值．
，
．（1）求动点N的轨迹C方程；（2）由直线y= -1上一点Q向曲线C引两条切线，切点分别为A，B，求证：AQ⊥BQ．