题目内容
已知 设函数
设函数

(Ⅰ)当 ,求函数
,求函数 的的值域;
的的值域;
(Ⅱ)当 时,若
时,若 ="8," 求函数
="8," 求函数 的值;
的值;
 设函数
设函数
(Ⅰ)当
 ,求函数
,求函数 的的值域;
的的值域;
|
 时,若
时,若 ="8," 求函数
="8," 求函数 的值;
的值;
(Ⅰ)函数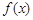 的值域为
的值域为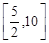 . (Ⅱ)
. (Ⅱ)  =
=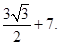
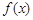 的值域为
的值域为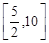 . (Ⅱ)
. (Ⅱ)  =
=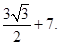
(I)先根据数量积的定义及向量的模的坐标表示以及降幂公式及两角和与差的恒等变换公式求出 ,再根据x的范围求值域.
,再根据x的范围求值域.
(II)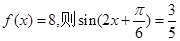 ,再根据
,再根据 ,确定出
,确定出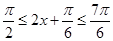 ,求出
,求出 然后把
然后把 转化为
转化为
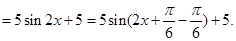 问题到此基本得以解决.
问题到此基本得以解决.
(Ⅰ)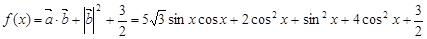
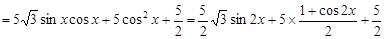
 ,
,
由
 得
得 ,所以
,所以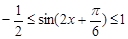 ,则函数
,则函数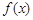 的值域为
的值域为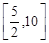 .
.
(Ⅱ) ,
,
 ; 所以
; 所以
 =
=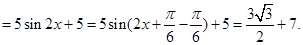
 ,再根据x的范围求值域.
,再根据x的范围求值域.(II)
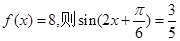 ,再根据
,再根据 ,确定出
,确定出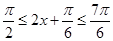 ,求出
,求出 然后把
然后把 转化为
转化为
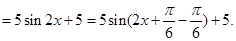 问题到此基本得以解决.
问题到此基本得以解决.(Ⅰ)
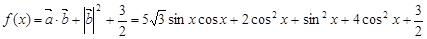
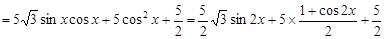
 ,
,由

 得
得 ,所以
,所以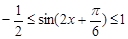 ,则函数
,则函数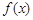 的值域为
的值域为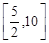 .
. (Ⅱ)
 ,
,  ; 所以
; 所以
 =
=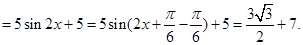

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
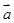 =(cosα,sinα) (0°≤α<360°),
=(cosα,sinα) (0°≤α<360°),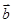 =(-
=(- ,
, ).
).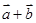 与
与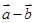 垂直;
垂直;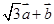 与
与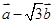 的模相等时,求角α.
的模相等时,求角α. .
. 的最小正周期;(2)求函数
的最小正周期;(2)求函数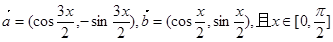 ,若
,若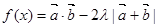 的最小值是
的最小值是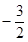 ,求实数
,求实数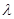 的值.
的值. 中,
中, 分别是角
分别是角 的对边,且
的对边,且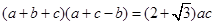
 ;
;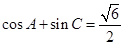 ,
, ,求
,求 的取值范围。
的取值范围。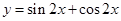 的图像,只需将曲线
的图像,只需将曲线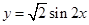 上所有的点( )
上所有的点( )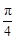 个单位
个单位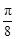 个单位
个单位  ,
, (0,π),则
(0,π),则 =
= 1
1

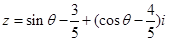 是纯虚数,则
是纯虚数,则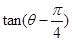 的值为( )
的值为( )
 或
或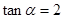 则
则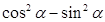 的值是( )
的值是( )