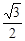题目内容
(本题满分9分)
设平面上向量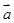 =(cosα,sinα) (0°≤α<360°),
=(cosα,sinα) (0°≤α<360°),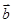 =(-
=(- ,
, ).
).
(1)试证:向量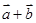 与
与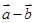 垂直;
垂直;
(2)当两个向量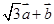 与
与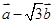 的模相等时,求角α.
的模相等时,求角α.
设平面上向量
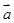 =(cosα,sinα) (0°≤α<360°),
=(cosα,sinα) (0°≤α<360°),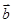 =(-
=(- ,
, ).
).(1)试证:向量
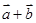 与
与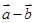 垂直;
垂直;(2)当两个向量
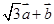 与
与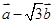 的模相等时,求角α.
的模相等时,求角α.(1)见解析;(2)α=30°,或α=210°.
本试题主要是考查了向量的数量积的运算,以及向量的数量积的性质的运用,以及三角函数的变形运用,和三角方程的求解的综合试题。
((1)根据已知要证明向量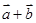 与
与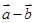 垂直,则利用数量积为零即可。
垂直,则利用数量积为零即可。
(2)由|a|=1,|b|=1,且| a+b|=|a-
a+b|=|a- b|,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值。
b|,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值。
解: (1)(a+b)·(a-b)=(cosα- ,sinα+
,sinα+ )·(cosα+
)·(cosα+ ,sinα-
,sinα- )
)
=(cosα- )(cosα+
)(cosα+ )+(sinα+
)+(sinα+ )(sinα-
)(sinα- )
)
=cos2α-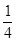 +sin2α-
+sin2α-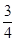 =0,
=0,
∴(a+b)⊥(a-b). ……4分
(2)由|a|=1,|b|=1,且| a+b|=|a-
a+b|=|a- b|,平方得(
b|,平方得( a+b)2=(a-
a+b)2=(a- b)2,
b)2,
整理得2a2-2b2+4 ab=0①.
ab=0①.
∵|a|=1,|b|=1,∴①式化简得a·b=0,
a·b=(cosα,sinα)·(- ,
, )=-
)=- cosα+
cosα+ sinα=0,即cos(60°+α)=0.
sinα=0,即cos(60°+α)=0.
∵0°≤α<360°,∴可得α=30°,或α=210°. ……9分
((1)根据已知要证明向量
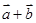 与
与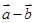 垂直,则利用数量积为零即可。
垂直,则利用数量积为零即可。(2)由|a|=1,|b|=1,且|
 a+b|=|a-
a+b|=|a- b|,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值。
b|,利用模相等,则平方后相等来解得关于角α的方程,然后解三角方程得到角的值。解: (1)(a+b)·(a-b)=(cosα-
 ,sinα+
,sinα+ )·(cosα+
)·(cosα+ ,sinα-
,sinα- )
)=(cosα-
 )(cosα+
)(cosα+ )+(sinα+
)+(sinα+ )(sinα-
)(sinα- )
)=cos2α-
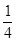 +sin2α-
+sin2α-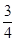 =0,
=0,∴(a+b)⊥(a-b). ……4分
(2)由|a|=1,|b|=1,且|
 a+b|=|a-
a+b|=|a- b|,平方得(
b|,平方得( a+b)2=(a-
a+b)2=(a- b)2,
b)2,整理得2a2-2b2+4
 ab=0①.
ab=0①.∵|a|=1,|b|=1,∴①式化简得a·b=0,
a·b=(cosα,sinα)·(-
 ,
, )=-
)=- cosα+
cosα+ sinα=0,即cos(60°+α)=0.
sinα=0,即cos(60°+α)=0.
∵0°≤α<360°,∴可得α=30°,或α=210°. ……9分

练习册系列答案
相关题目
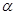 终边上一点P(-4,3),求
终边上一点P(-4,3),求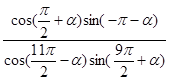 的值
的值 设函数
设函数
 ,求函数
,求函数 的的值域;
的的值域; 的值;
的值;
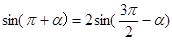 ,求
,求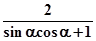 的值.
的值. 的值为( )
的值为( )



 则
则 的值是 .
的值是 . sinB-cosC的取值范围为___________.
sinB-cosC的取值范围为___________.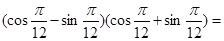
 的值是( )
的值是( )