题目内容
求下列函数的值域:
(1)y=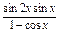 ;
;
(2)y=sinx+cosx+sinxcosx;
(3)y=2cos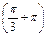 +2cosx.
+2cosx.
(1)y=
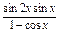 ;
;(2)y=sinx+cosx+sinxcosx;
(3)y=2cos
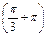 +2cosx.
+2cosx.(1)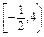 (2)
(2)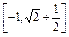 (3) [-2
(3) [-2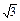 ,2
,2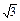 ]
]
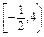 (2)
(2)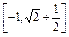 (3) [-2
(3) [-2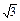 ,2
,2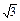 ]
](1)y=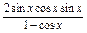 =
=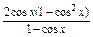
=2cos2x+2cosx=2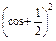 -
-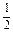 .
.
于是当且仅当cosx=1时取得ymax=4,但cosx≠1,
∴y<4,且ymin=-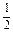 ,当且仅当cosx=-
,当且仅当cosx=-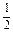 时取得.
时取得.
故函数值域为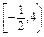 .
.
(2)令t=sinx+cosx,则有t2=1+2sinxcosx,即sinxcosx=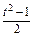 .
.
有y=f(t)=t+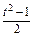 =
=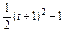 .
.
又t=sinx+cosx=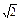 sin
sin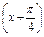 ,∴-
,∴-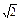 ≤t≤
≤t≤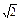 .
.
故y="f(t)="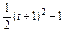 (-
(-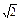 ≤t≤
≤t≤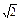 ),
),
从而知:f(-1)≤y≤f(2),即-1≤y≤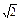 +
+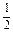 .即函数的值域为
.即函数的值域为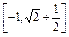 .
.
(3)y=2cos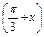 +2cosx
+2cosx
=2cos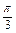 cosx-2sin
cosx-2sin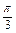 sinx+2cosx
sinx+2cosx
=3cosx-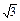 sinx=2
sinx=2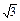
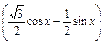
=2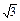 cos
cos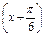 .
.
∵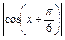 ≤1
≤1
∴该函数值域为[-2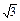 ,2
,2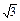 ].
].
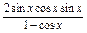 =
=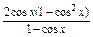
=2cos2x+2cosx=2
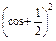 -
-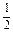 .
.于是当且仅当cosx=1时取得ymax=4,但cosx≠1,
∴y<4,且ymin=-
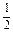 ,当且仅当cosx=-
,当且仅当cosx=-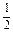 时取得.
时取得.故函数值域为
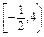 .
.(2)令t=sinx+cosx,则有t2=1+2sinxcosx,即sinxcosx=
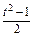 .
.有y=f(t)=t+
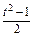 =
=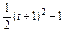 .
.又t=sinx+cosx=
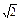 sin
sin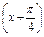 ,∴-
,∴-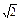 ≤t≤
≤t≤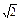 .
.故y="f(t)="
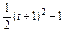 (-
(-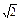 ≤t≤
≤t≤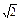 ),
),从而知:f(-1)≤y≤f(2),即-1≤y≤
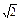 +
+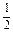 .即函数的值域为
.即函数的值域为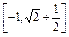 .
.(3)y=2cos
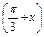 +2cosx
+2cosx=2cos
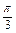 cosx-2sin
cosx-2sin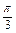 sinx+2cosx
sinx+2cosx=3cosx-
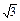 sinx=2
sinx=2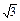
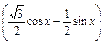
=2
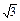 cos
cos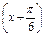 .
.∵
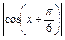 ≤1
≤1∴该函数值域为[-2
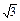 ,2
,2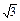 ].
].
练习册系列答案
相关题目
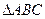
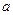
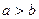 ,则
,则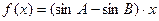 在R上是增函数;
在R上是增函数;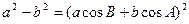 ,则
,则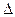 ABC是
ABC是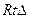 ;
;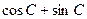 的最小值为
的最小值为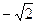 ;
;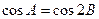 ,则A=B;
,则A=B; ,则
,则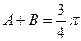 ,
, 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 .
. 的值; (Ⅱ)求
的值; (Ⅱ)求 的最大值.
的最大值.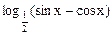 (Ⅰ)求它的定义域和值域;(Ⅱ)判断它的奇偶性;(Ⅲ)判断它的周期性。
(Ⅰ)求它的定义域和值域;(Ⅱ)判断它的奇偶性;(Ⅲ)判断它的周期性。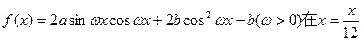 时取最大值2。
时取最大值2。 是集合
是集合 中的任意两个元素,
中的任意两个元素, 的最小值为
的最小值为 。
。 的值。
的值。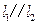 ,
,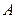 是
是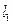 ,
,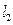 之间的一定点,并且
之间的一定点,并且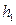 ,
,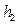 .
.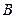 是直线
是直线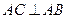 .且使
.且使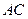 与直线
与直线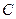 ,求
,求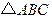 面积的最小值.
面积的最小值.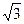 cos2x-2.
cos2x-2.
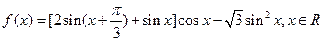
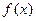 的最小正周期;
的最小正周期;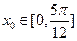 ,使不等式
,使不等式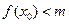 成立,求实数m的取值范围.
成立,求实数m的取值范围.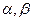 为锐角且
为锐角且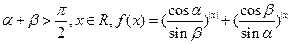
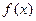 在定义域上为递增函数
在定义域上为递增函数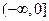 上为增函数,在
上为增函数,在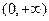 上为减函数
上为减函数