题目内容
设函数f(x)=ax2+lnx.
(Ⅰ)当a=-1时,求函数y=f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)已知a<0,若函数y=f(x)的图象总在直线y=-![]() 的下方,求a的取值范围;
的下方,求a的取值范围;
(Ⅲ)记![]() 为函数f(x)的导函数.若a=1,试问:在区间[1,10]上是否存在k(k<100)个正数x1,x2,x3…xk,使得
为函数f(x)的导函数.若a=1,试问:在区间[1,10]上是否存在k(k<100)个正数x1,x2,x3…xk,使得![]() 成立?请证明你的结论.
成立?请证明你的结论.
答案:
解析:
解析:
|
解:(Ⅰ)当 所以切线的斜率为 又 故所求的切线方程为: (Ⅱ) 令 当 故 所以 由题意有 所以 (Ⅲ)当 ∵当 即 又 所以,对任意的 所以 又因为 故在区间 |

练习册系列答案
相关题目
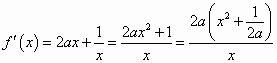 ,
,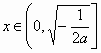 时,
时,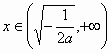 时,
时,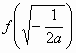 =
= (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方