题目内容
已知数列{an},满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),则{an}的通项an= .
【答案】分析:先根据已知的递推式,求得an+1=a1+2a2+3a3+…+(n-1)an-1+nan,减去已知等式,求得an+1=(n+1)an,进而可求得每相邻两项的比,然后用叠乘法求得数列的通项公式.
解答:解:由已知,得an+1=a1+2a2+3a3+…+(n-1)an-1+nan,用此式减去已知式,得
当n≥2时,an+1-an=nan,即an+1=(n+1)an,又a2=a1,
所以a1=1,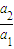 =1,
=1,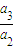 =3,
=3,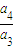 =4,…
=4,… =n,上式相乘求得an=
=n,上式相乘求得an=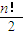 (n≥2)
(n≥2)
故答案为:an= .
.
点评:本题主要考查了数列的递推式.对于an+1=f(n)an的形式,一般是把原递推公式转化为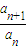 ,利用累乘法(逐商相乘法)求解.
,利用累乘法(逐商相乘法)求解.
解答:解:由已知,得an+1=a1+2a2+3a3+…+(n-1)an-1+nan,用此式减去已知式,得
当n≥2时,an+1-an=nan,即an+1=(n+1)an,又a2=a1,
所以a1=1,
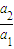 =1,
=1,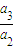 =3,
=3,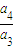 =4,…
=4,… =n,上式相乘求得an=
=n,上式相乘求得an=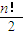 (n≥2)
(n≥2)故答案为:an=
 .
.点评:本题主要考查了数列的递推式.对于an+1=f(n)an的形式,一般是把原递推公式转化为
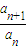 ,利用累乘法(逐商相乘法)求解.
,利用累乘法(逐商相乘法)求解. 
练习册系列答案
 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目