题目内容
已知二次函数的图象过点(-3,0),(1,0),且顶点到x轴的距离等于2,求此二次函数的表达式.
分析:解法一:设函数为交点式,利用二次函数图象的顶点到x轴的距离2,可得函数解析式;
解法二:设函数为顶点式,利用函数图象过点(1,0),可得函数解析式.
解法二:设函数为顶点式,利用函数图象过点(1,0),可得函数解析式.
解答:解法一:∵二次函数的图象过点(-3,0),(1,0),
∴可设二次函数为y=a(x+3)(x-1)(a≠0),
展开,得 y=ax2+2ax-3a,
顶点的纵坐标为
=-4a,
由于二次函数图象的顶点到x轴的距离2,
∴|-4a|=2,即a=±
.
所以,二次函数的表达式为y=
x2+x-
,或y=-
x2-x+
.
解法二:∵二次函数的图象过点(-3,0),(1,0),
∴对称轴为直线x=-1.
又顶点到x轴的距离为2,
∴顶点的纵坐标为2,或-2.
于是可设二次函数为y=a(x+1)2+2,或y=a(x+1)2-2,
由于函数图象过点(1,0),
∴0=a(1+1)2+2,或0=a(1+1)2-2.
∴a=-
,或a=
.
所以,所求的二次函数为y=-
(x+1)2+2,或y=
(x+1)2-2.
∴可设二次函数为y=a(x+3)(x-1)(a≠0),
展开,得 y=ax2+2ax-3a,
顶点的纵坐标为
| -12a2-4a2 |
| 4a |
由于二次函数图象的顶点到x轴的距离2,
∴|-4a|=2,即a=±
| 1 |
| 2 |
所以,二次函数的表达式为y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解法二:∵二次函数的图象过点(-3,0),(1,0),
∴对称轴为直线x=-1.
又顶点到x轴的距离为2,
∴顶点的纵坐标为2,或-2.
于是可设二次函数为y=a(x+1)2+2,或y=a(x+1)2-2,
由于函数图象过点(1,0),
∴0=a(1+1)2+2,或0=a(1+1)2-2.
∴a=-
| 1 |
| 2 |
| 1 |
| 2 |
所以,所求的二次函数为y=-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查函数解析式的求法,解题的关键是正确设出函数的解析式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象过点
的图象过点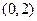 ,其导函数为
,其导函数为 ,数列
,数列
 项和为
项和为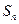 ,点
,点 在函数
在函数 .
. 的解析式;
的解析式; ,求数列
,求数列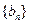 的前
的前 .
.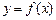 的图象过点(0,
的图象过点(0, ),且
),且 的解集为(1,3)。
的解集为(1,3)。 的解析式;
的解析式; ,
, 的最值。
的最值。 的图象过点(1,13),图像关于直线
的图象过点(1,13),图像关于直线 对称。
对称。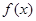 的解析式。
的解析式。 ,
, ,
, 的零点有三个,求实数
的零点有三个,求实数 的取值范围;
的取值范围; 在[
在[ ,2]上的最小值。
,2]上的最小值。 的图象过点(0,—3),且
的图象过点(0,—3),且 的解集(1,3)。
的解集(1,3)。 的解析式;
的解析式; 时,恒有
时,恒有 求实数t的取值范围。
求实数t的取值范围。