题目内容
(本题满分16分,第1小题4分,第2小题6分,第3小题6分)
设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为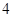 的直角三角形.过B1作直线l交椭圆于P、Q两点.
的直角三角形.过B1作直线l交椭圆于P、Q两点.
(1) 求该椭圆的标准方程;
(2) 若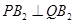 ,求直线l的方程;
,求直线l的方程;
(3) 设直线l与圆O:x2+y2=8相交于M、N两点,令|MN|的长度为t,若t∈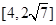 ,求△B2PQ的面积
,求△B2PQ的面积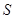 的取值范围.
的取值范围.
(1)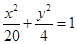 ;(2)x+2y+2=0和x–2y+2=0;(3)
;(2)x+2y+2=0和x–2y+2=0;(3)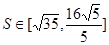 。
。
【解析】
试题分析:(1)设所求椭圆的标准方程为 ,右焦点为
,右焦点为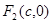 .
.
因△AB1B2是直角三角形,又|AB1|=|AB2|,故∠B1AB2=90º,得c=2b…………1分
在Rt△AB1B2中,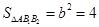 ,从而
,从而 .………………3分
.………………3分
因此所求椭圆的标准方程为: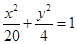 …………………………………………4分
…………………………………………4分
(2)由(1)知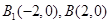 ,由题意知直线的倾斜角不为0,故可设直线的方程为:
,由题意知直线的倾斜角不为0,故可设直线的方程为: ,代入椭圆方程得
,代入椭圆方程得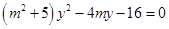 ,…………………………6分
,…………………………6分
设P(x1, y1)、Q(x2,
y2),则y1、y2是上面方程的两根,因此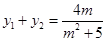 ,
,
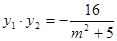 ,又
,又 ,所以
,所以
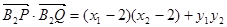
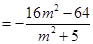 ………………………………8分
………………………………8分
由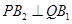 ,得
,得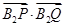 =0,即
=0,即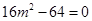 ,解得
,解得 ;
;
所以满足条件的直线有两条,其方程分别为:x+2y+2=0和x–2y+2=0……………………10分
(3) 当斜率不存在时,直线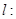
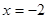 ,此时
,此时 ,
, ………………11分
………………11分
当斜率存在时,设直线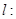
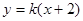 ,则圆心
,则圆心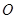 到直线的距离
到直线的距离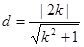 ,
,
因此t= ,得
,得 ………………………………………13分
………………………………………13分
联立方程组: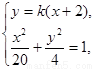 得
得 ,由韦达定理知,
,由韦达定理知,
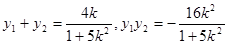 ,所以
,所以 ,
,
因此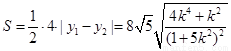 .
.
设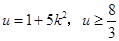 ,所以
,所以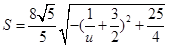 ,所以
,所以 …15分
…15分
综上所述:△B2PQ的面积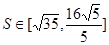 ……………………………………………16分
……………………………………………16分
考点:椭圆的简单性质;圆的简单性质;直线与椭圆的综合应用。
点评:直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.

 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,
,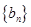 是等差数列,且
是等差数列,且 ,求非零常数
,求非零常数 ;
; ,求证:
,求证: .
.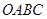 中,已知过点
中,已知过点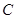 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若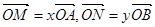 。
。 与
与 的关系为
的关系为 ;
; ,定义在
,定义在 上的偶函数
上的偶函数 ,当
,当 时
时 ,且函数
,且函数 对称,求证:
对称,求证: ,并求
,并求 时的解析式;
时的解析式; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。 、
、 为坐标平面
为坐标平面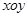 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点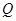 (异于
(异于 ,点
,点 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
; 在椭圆
在椭圆 上,试问:点
上,试问:点 、
、 是圆
是圆 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 是
是 轴正方向的单位向量,设
轴正方向的单位向量,设 =
= ,
,  =
= ,且满足
,且满足 .
.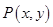 的轨迹方程;
的轨迹方程; 的直线
的直线 交上述轨迹于
交上述轨迹于 两点,且
两点,且 ,求直线
,求直线