题目内容
在平面上，若两个正三角形的边长之比为
，则它们的面积之比为
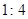；类似地，在空间内，若两个正四面体的棱长之比为，则它们的体积
1：8
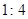解析试题分析：根据题意，两个正三角形的边长之比为，则它们的面积之比为相似比的平方；类似地，在空间内，若两个正四面体的棱长之比为，则它们的体积比为相似比的立方，那么即为1：8，故答案为1：8.
考点：正四面体，类比推理
点评：主要考查了类比推理，以及四面体的体积公式的运用，属于基础题。
练习册系列答案
相关题目
的第二步中，当n=k+1时等式左边与n=k时的等式左边的差等于 .
，则依次类推可得
；
中,若
是数列
项积,则有
也成等比数列，且公比为
；类比上述结论，相应的在公差为3的等差数列
中，若
是
，把四面体V-BCD与三角形作类比，设二面角V-BC-D，V-CD-B， V-BD-C，C-VB-D，B-VC-D，B-VD-C的大小依次为
我们可以得到“四面体的余弦定理”：_____________________.（只需写出一个关系式）
的通项公式
,记
,试通过计算
的值,推测出
，
_________.
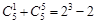
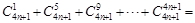