题目内容
如图,过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为
答案:
解析:
解析:
| 答案:解:由题意, 整理得: 设交点A(x1,y1),B(x2,y2),中点M(x0,y0),而中点在直线 ∴ 求得:k=-1,将k=-1代入①, F(c,0)关于直线l:y=-x+1的对称点(1,1-c)在椭圆上,代入椭圆方程: ∴1+2(1-c)2-2c2=0, ∴ ∴所求椭圆为C:
|

练习册系列答案
相关题目
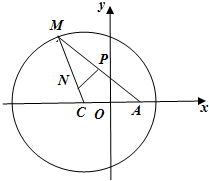 已知圆C:(x+1)2+y2=8.
已知圆C:(x+1)2+y2=8.