题目内容
已知函数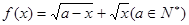 ,对定义域内任意
,对定义域内任意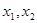 ,满足
,满足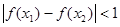 ,则正整数
,则正整数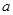 的取值个数是
的取值个数是
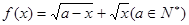 ,对定义域内任意
,对定义域内任意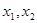 ,满足
,满足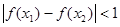 ,则正整数
,则正整数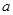 的取值个数是
的取值个数是 5
分析:由条件对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,问题可以转化为f(x)max-f(x)min<1,因此求函数的最值是关键.求最值时,利用换元法求解。
解答:
由题意,
 =
=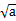 cosα,
cosα, =
=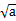 sinα(α∈[0,π/2],
sinα(α∈[0,π/2],f(x)=
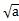 cosα+
cosα+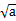 sinα=
sinα=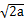 sin(α +π/4),
sin(α +π/4),从而有f(x)max=
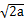 ,f(x)min=
,f(x)min=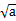 ,
,∴
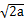 -
-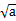 <1解得a<3+2
<1解得a<3+2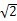 ,
,∵a∈N*,
∴a=1,2,3,4,5,
∴正整数
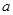 的取值个数是5个。
的取值个数是5个。点评:解答时等价转化是解题的关键,求解函数的最值运用三角换元法,应注意参数角的范围。

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 ,则函数
,则函数 在其定义域内的零点有( )
在其定义域内的零点有( ) 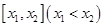 的长度为
的长度为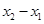 .已知函数
.已知函数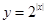 的定义域为
的定义域为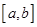 ,值域为
,值域为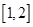 ,记区间
,记区间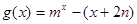 的零点个数是 ( )
的零点个数是 ( ) 的定义域为( )
的定义域为( )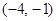



 +
+ 的定义域
的定义域 
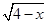 的定义域是( ).
的定义域是( ).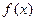 的定义域是
的定义域是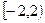 ,则函数
,则函数 的定义域是_________
的定义域是_________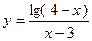 的定义域是
的定义域是 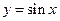 的定义域为
的定义域为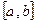 ,值域为
,值域为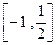 ,则
,则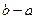 的最大值与最小值之和等于
的最大值与最小值之和等于