题目内容
将圆x2+y2=1按向量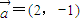 平移后,恰好与直线x-y+b=0相切,则实数b的值为( )
平移后,恰好与直线x-y+b=0相切,则实数b的值为( )A.
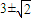
B.-
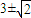
C.
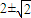
D.-
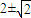
【答案】分析:先求出平移后圆的方程,并根据方程求出圆心坐标和圆的半径,利用此圆和直线x-y+b=0相切,圆心到直线的距离等于半径,建立等式,解方程求出实数b的值.
解答:解:将圆x2+y2=1按向量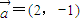 平移后得到的圆方程为(x-2)2+(y+1)2=1,
平移后得到的圆方程为(x-2)2+(y+1)2=1,
表示圆心在(2,-1),半径等于1的圆,由此圆和直线x-y+b=0相切,圆心到直线的距离等于半径得:
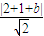 =1,∴b=-3±
=1,∴b=-3± ,
,
故选B.
点评:本题考查曲线的平移问题以及直线和圆相切的条件.
解答:解:将圆x2+y2=1按向量
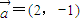 平移后得到的圆方程为(x-2)2+(y+1)2=1,
平移后得到的圆方程为(x-2)2+(y+1)2=1,表示圆心在(2,-1),半径等于1的圆,由此圆和直线x-y+b=0相切,圆心到直线的距离等于半径得:
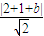 =1,∴b=-3±
=1,∴b=-3± ,
,故选B.
点评:本题考查曲线的平移问题以及直线和圆相切的条件.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
将圆x2+y2=1按向量
=(2,-1)平移后,恰好与直线x-y+b=0相切,则实数b的值为( )
| a |
A、3±
| ||
B、-3±
| ||
C、2±
| ||
D、-2±
|
 平移后,恰好与直线x-y+b=0相切,则实数b的值为( )
平移后,恰好与直线x-y+b=0相切,则实数b的值为( )


