题目内容
设F1,F2分别是椭圆![]() (a>b>0)的左、右焦点
(a>b>0)的左、右焦点
(1)若椭圆C上的点![]() 到F1,F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
到F1,F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点P是(1)中所得椭圆上的动点,![]() ,求PQ的最大值;
,求PQ的最大值;
(3)已知椭圆具有性质:若M,N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM,PN的斜率都存在,并记为KPM、KPN时,那么KPM与KPN之积是与点P位置无关的定值.试对双曲线![]() 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.
答案:
解析:
解析:
|
解:(1)椭圆 即 所以椭圆 设 又 类似的性质为:若 设点 |

练习册系列答案
相关题目
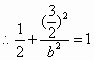 ,解得
,解得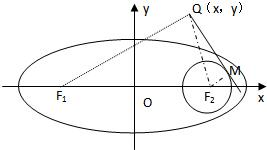 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C: