题目内容
双曲线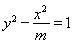 的离心率
的离心率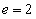 ,则以双曲线的两条渐近线与抛物线
,则以双曲线的两条渐近线与抛物线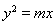 的交点为顶点的三角形的面积为( )
的交点为顶点的三角形的面积为( )
(A)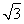 (B)
(B)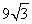 (C)
(C)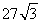 (D)
(D)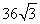
【答案】
C
【解析】
试题分析:由题可知 ,
,
所以,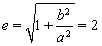 ,即
,即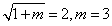 ,
,
故双曲线的两条渐近线为 ,抛物线方程为
,抛物线方程为 ,
,
联立方程组 可得渐近线与抛物线的交点为
可得渐近线与抛物线的交点为 ,
,
由抛物线的对称性可知 的面积为
的面积为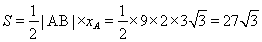 .
.
故选 .
.
考点:双曲线的几何性质,直线与抛物线的位置关系,三角形面积公式.

练习册系列答案
相关题目
已知F1、F2是两个定点,点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点,并且PF1⊥PF2,e1和e2分别是上述椭圆和双曲线的离心率,则有( )
| A、e12+e22=2 | ||||||||
| B、e12+e22=4 | ||||||||
C、
| ||||||||
D、
|
 中,
中, 且
且 ,
,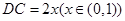 . 以
. 以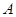 ,
, 为焦点,且过点
为焦点,且过点 的双曲线的离心率为
的双曲线的离心率为 ;以
;以 ,
, ,则
,则 的取值范围为( )
的取值范围为( )
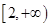 B.
B. C.
C. D.
D.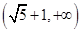
 中,
中, ,且
,且 . 设
. 设 ,
, ,以
,以 ,
, 为焦点且过点
为焦点且过点 的双曲线的离心率为
的双曲线的离心率为 ,以
,以 ,
, ,则( )
,则( )
 的增大,
的增大, 为定值
为定值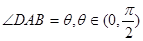 ,以A,B为焦点且过点D的双曲线的离心率为
,以A,B为焦点且过点D的双曲线的离心率为 ,以C,D为焦点且过点A的椭圆的离心率为
,以C,D为焦点且过点A的椭圆的离心率为 ,则 ( )
,则 ( )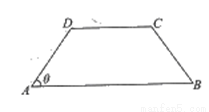
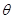 的增大,
的增大, 为定值
为定值