题目内容
(08年芜湖一中)已知在平面直角坐标系![]() 中,若在曲线
中,若在曲线![]() 的方程
的方程![]() 中以
中以![]()
![]() 为正实数)代替
为正实数)代替![]() 得到曲线
得到曲线![]() 的方程
的方程![]() ,则称曲线
,则称曲线![]() 关于原点“伸缩”,变换
关于原点“伸缩”,变换![]() 称为“伸缩变换”,
称为“伸缩变换”,![]() 称为伸缩比.
称为伸缩比.
(1)已知曲线![]() 的方程为
的方程为![]() ,伸缩比
,伸缩比![]() ,求
,求![]() 关于原点“伸缩变换”后所得曲线
关于原点“伸缩变换”后所得曲线![]() 的标准方程;
的标准方程;
(2)射线![]() 的方程
的方程![]() ,如果椭圆
,如果椭圆![]()
![]() 经“伸缩变换”后得到椭圆
经“伸缩变换”后得到椭圆![]() ,若射线
,若射线![]() 与椭圆
与椭圆![]() 分别交于两点
分别交于两点![]() ,且
,且![]() ,求椭圆
,求椭圆![]() 的标准方程;
的标准方程;
(3)对抛物线![]() ,作变换
,作变换![]() ,得抛物线
,得抛物线![]() ;对
;对![]() 作变换
作变换![]() 得抛物线
得抛物线![]() ,如此进行下去,对抛物线
,如此进行下去,对抛物线![]() 作变换
作变换![]() ,得抛物线
,得抛物线![]()
![]() .若
.若![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() .
.
【解】(1) 由条件得![]()
![]() ,得
,得![]() :
: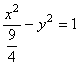 ;(2分)
;(2分)
(2) ![]() “伸缩变换”,对
“伸缩变换”,对![]() 作变换
作变换![]() ,得到
,得到![]()
![]() ,(3分)
,(3分)
解方程组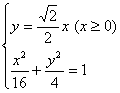 得点A的坐标为
得点A的坐标为![]() ;(4分)解方程组
;(4分)解方程组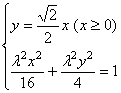 得点B的坐标为
得点B的坐标为![]() ;(5分)
;(5分)![]() =
=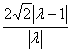 =
=![]() ,化简后得
,化简后得![]() ,解得
,解得![]() ,因此椭圆
,因此椭圆![]() 的方程为
的方程为![]() 或
或![]() .(9分)
.(9分)
(3)对![]() :
:![]() 作变换
作变换![]() 得抛物线
得抛物线![]() :
:![]() 得
得![]() ,又
,又![]() ,即
,即![]() ,(11分)
,(11分)![]()
![]()
![]()
![]()
![]() =
=![]() ,则
,则![]() ,(13分)
,(13分)
(或解:![]()
![]()
![]() )
)
又![]() ,
,![]() .(14分)
.(14分)

练习册系列答案
相关题目