题目内容
(理科做)函数y=f(x)(x∈R)满足:对一切 ,当x∈[0,1]时,
,当x∈[0,1]时, ,则
,则 = .
= .
【答案】分析:根据对一切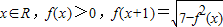 ,可得函数的周期为2,利用函数的解析式,即可得到结论、
,可得函数的周期为2,利用函数的解析式,即可得到结论、
解答:解:∵对一切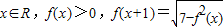 ,
,
∴f2(x+1)+f2(x)=7,
∴f2(x+2)+f2(x+1)=7
两式相减得:f2(x+2)=f2(x),即f(x+2)=f(x)
∴函数的周期为2
∴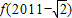 =
=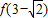 =
=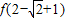 =
=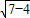 =
=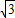
故答案为: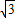
点评:本题主要考查了函数的值,以及函数的周期性,同时考查转化的思想,属于中档题.
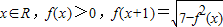 ,可得函数的周期为2,利用函数的解析式,即可得到结论、
,可得函数的周期为2,利用函数的解析式,即可得到结论、解答:解:∵对一切
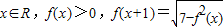 ,
,∴f2(x+1)+f2(x)=7,
∴f2(x+2)+f2(x+1)=7
两式相减得:f2(x+2)=f2(x),即f(x+2)=f(x)
∴函数的周期为2
∴
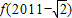 =
=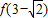 =
=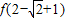 =
=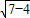 =
=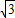
故答案为:
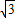
点评:本题主要考查了函数的值,以及函数的周期性,同时考查转化的思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目