题目内容
如图,在三棱锥V-ABC中,VC![]() 底面ABC,AC
底面ABC,AC![]() BC,D是AB的中点,且AC=BC=VC=
BC,D是AB的中点,且AC=BC=VC= ![]()
(1)求证:平面VAB![]() 平面VCD;
平面VCD;
(2)若线段AB上的一点E, 使得直线VD与平面VCE所成的角的正弦为![]() ,试确定E的位置
,试确定E的位置

(1)略(2)点E位于线段AD的中点或线段BD 的中点.
解析:
方法1:(1)∵AC=BC,∴![]() 是等腰三角形,
是等腰三角形,
又D是AB的中点,∴![]() ,
,
又![]() 底面
底面![]() ,∴
,∴![]() 。于是
。于是![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() 。 …………5分
。 …………5分
(2)过点D在平面ABC内作![]() 于F,则由题意知
于F,则由题意知![]() 平面VCE。连接VF,于是
平面VCE。连接VF,于是![]() 就是直线VD与平面VCE所成的角。 …………7分
就是直线VD与平面VCE所成的角。 …………7分
在![]() 中,
中,![]() ;
;
又![]() VD=
VD= ![]() , ∴
, ∴![]() …………9分
…………9分
在![]() 中可求出DE=1 ………11分
中可求出DE=1 ………11分
故知点E位于线段AD的中点或线段BD 的中点. ………12分
方法2:(1)以CA、CB、CV所在的直线分别为x轴、 y轴、z轴,建立如图所示的空间直角坐标系,
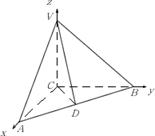
则![]() ,
,![]() ,
, ![]() ,
, ![]()
于是 ![]() ,
, ![]()
∴![]() =0, ∴
=0, ∴![]()
又![]() 底面
底面![]() ,
, ![]() , 于是
, 于是![]() 平面
平面![]()
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]()
(2)由(1)知 ![]() ,
,![]()
因为E点在线段AB上,而AB线上的点都满足![]() ,且z=0.
,且z=0.
所以可设![]() ,那么
,那么![]()
另设平面VCE的法向量![]() ,
,
由![]() ,
, ![]() ,可求n=0,
,可求n=0, ![]()
又因为直线VD与平面VCE所成的角的正弦为![]() ,
,
所以![]()
解之有x= ![]() 或x=
或x= ![]()
故点![]() 或
或![]() , 分别为线段BD的中点和线段AD的中点
, 分别为线段BD的中点和线段AD的中点

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4. 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°. .
.