题目内容
在直角坐标系中,定义两点 之间的“直角距离”为
之间的“直角距离”为 。现有下列命题:
。现有下列命题:
①若P,Q是x轴上两点,则 ;
;
②已知P(1,3),Q( )(
)( ),则d(P,Q)为定值;
),则d(P,Q)为定值;
③原点O到直线 上任一点P的直角距离d(O,P)的最小值为
上任一点P的直角距离d(O,P)的最小值为 ;
;
④设A(x,y)且 ,若点A是在过P(1,3)与Q(5,7)的直线上,且点A到点P与Q的“直角距离”之和等于8,那么满足条件的点A只有5个.
,若点A是在过P(1,3)与Q(5,7)的直线上,且点A到点P与Q的“直角距离”之和等于8,那么满足条件的点A只有5个.
其中的真命题是.(写出所有真命题的序号)
①②④
解析试题分析:对①由所给定义知,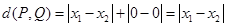 ,故正确;
,故正确;
对②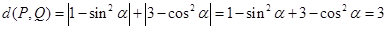 为定值,所以正确;
为定值,所以正确;
对③设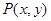 ,则
,则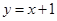 .
.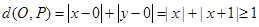 ,即最小值为
,即最小值为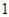 ;故错;
;故错;
④若点A是在线段PQ上,则满足点A到点P与Q的“直角距离”之和等于8,这样的整点有以下5个:
(1,3),(2,4),(3,5),(4,6),(5,7).若点A是在线段PQ或QP延长线上,点A到点P与Q的“直角距离”之和大于8.所以满足条件的点A只有5个.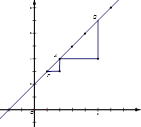
考点:新定义.

练习册系列答案
相关题目
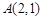 ,且与直线
,且与直线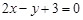 平行的直线方程为 .
平行的直线方程为 . ,
, ,若直线
,若直线 与
与 的夹角为
的夹角为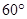 ,则
,则 = .
= . 中,若圆
中,若圆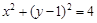 上存在
上存在 ,
, 两点,且弦
两点,且弦 的中点为
的中点为 ,则直线
,则直线 的方程为 .
的方程为 . 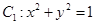 与圆
与圆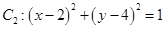 ,过动点
,过动点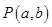 分别作圆
分别作圆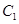 、圆
、圆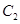 的切线
的切线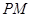 、
、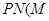 、
、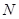 分别为切点),若
分别为切点),若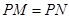 ,则
,则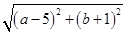 的最小值是 .
的最小值是 . 的圆心
的圆心 ,且与直线
,且与直线 垂直的直线方程是 .
垂直的直线方程是 .