题目内容
12.△ABC中,若(sinA+sinB+sinC )(sinA+sinB-sinC)=sinAsinB,则C=$\frac{2π}{3}$.分析 利用正弦定理以及余弦定理化简表达式,求解C即可.
解答 解:由正弦定理(sinA+sinB+sinC )(sinA+sinB-sinC)=sinAsinB,
化为:(a+b+c)(a+b-c)=ab,
可得a2+b2-c2=-ab,
则:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$,
C=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查余弦定理以及正弦定理的应用,考查三角形的解法,是基础题.

练习册系列答案
相关题目
5.下列函数中,y的最小值为4的是( )
| A. | y=x+$\frac{4}{x}$ | B. | y=2(2x+2-x) | ||
| C. | y=$\frac{2({x}^{2}+5)}{\sqrt{{x}^{2}+4}}$ | D. | y=sinx+$\frac{4}{sinx}$(0<x<π) |
4.若函数f(x)的定义域为[-1,1],则y=f(x)的图象与y轴( )
| A. | 可能没有交点 | B. | 有且仅有一个交点 | ||
| C. | 可能有两个交点 | D. | 可能有无数个交点 |
17.函数y=$\frac{1}{1-\frac{1}{x}}$的定义域是( )
| A. | {x|x∈R且x≠0} | B. | {x|x∈R且x≠1} | C. | {x|x∈R且x≠0且x≠1} | D. | {x|x∈R且x≠0或x≠1} |
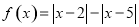 .
.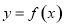 的值域;
的值域; 的解集.
的解集.