题目内容
【题目】设 .
.
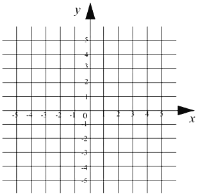
(1)在图的直角坐标系中画出f(x)的图象;
(2)若f(t)=2,求t值;
(3)求函数f(x)的最小值.
【答案】(1)见解析; (2)t=-2或t=![]() ,或t=2; (3)-1.
,或t=2; (3)-1.
【解析】
(1)根据分段函数的解析式,分三段画图,即可得到函数的图象;
(2)对t分三种情况讨论,得出相应的方程求解,即可得到答案;
(3)由(1)中函数的图象,结合图象,即可得到函数的最小值.
(1)f(x)的图象如右边:

(2)当t≤-1时,f(t)=-t=2,∴t=-2;
当-1<t<2时,f(t)=t2-1=2,解得:t=![]() ;
;
当t≥2时,f(t)=t=2,∴t=2,
综上所述:t=-2或t=![]() ,或t=2.
,或t=2.
(3)由图可知:当x∈(-1,2)时,f(x)=x2-1≥-1,
所以函数f(x)的最小值为-1.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(其中16名女员工,14名男员工)的得分,如下表:
女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
(Ⅰ)现求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女 | 16 | ||
男 | 14 | ||
合计 | 30 |
(Ⅱ)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
| 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式:![]()