题目内容
已知函数f(x)=log2(1-x)-log2(1+x).
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)方程f(x)=x+1是否有根?如果有根x0,请求出一个长度为
的区间(a,b),使x0∈(a,b);如果没有,请说明理由?(注:区间(a,b)的长度=b-a).
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)方程f(x)=x+1是否有根?如果有根x0,请求出一个长度为
| 1 |
| 4 |
(1)要使函数有意义,则
,
∴-1<x<1,故函数的定义域为(-1,1)
(2)∵f(-x)=log2(1+x)-log2(1-x)=-f(x),
∴f(x)为奇函数.
(3)由题意知方程f(x)=x+1?log2(1-x)-log2(1+x)=x+1,可化为(x+1)2x+1+x-1=0
设g(x)=(x+1)2x+1+x-1,x∈(-1,1)
则g(-
)=
×2
-
-1=
<0,g(0)=2-1=1>0,
所以g(-
)g(0)<0,故方程在(-
,0)上必有根;
又因为g(-
)=
×2
-
-1=
=
>0,
所以g(-
)g(-
)<0,故方程在(-
,-
)上必有一根.
所以满足题意的一个区间为(-
,-
).
|
∴-1<x<1,故函数的定义域为(-1,1)
(2)∵f(-x)=log2(1+x)-log2(1-x)=-f(x),
∴f(x)为奇函数.
(3)由题意知方程f(x)=x+1?log2(1-x)-log2(1+x)=x+1,可化为(x+1)2x+1+x-1=0
设g(x)=(x+1)2x+1+x-1,x∈(-1,1)
则g(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
所以g(-
| 1 |
| 2 |
| 1 |
| 2 |
又因为g(-
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
34
| ||
| 4 |
4
| ||||
| 4 |
所以g(-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
所以满足题意的一个区间为(-
| 1 |
| 2 |
| 1 |
| 4 |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
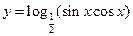 的递减区间是 .
的递减区间是 .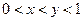 ,
,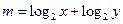 ,则有
,则有
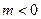 B
B 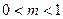 C
C 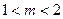 D
D